1 二元一次方程组的几何解释

考虑二元一次方程组：

1.1 二维行图像

按行将方程写成矩阵形式：

\begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix}- 系数矩阵（A）：方程系数按行构成一个矩阵

\begin{bmatrix} x \\ y \end{bmatrix}- 未知向量（x）：方程未知数按列构成一个向量

\begin{bmatrix} 0 \\ 3 \end{bmatrix} - 向量（b）：等号右侧的结果按列构成一个向量

从行的角度看，这是两条直线，交点即为解。 通过行图像求解：

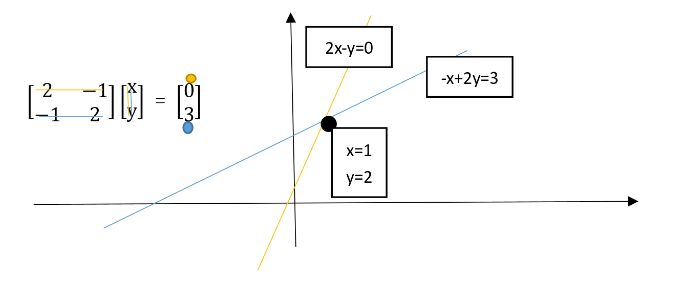
1.2 二维列图像

按列将方程写成线性组合：

此时问题转化成，将向量\begin{bmatrix} 2 \\ -1 \end{bmatrix}与向量\begin{bmatrix} -1 \\ 2 \end{bmatrix}正确组合，使得结果为\begin{bmatrix} 0 \\ 3 \end{bmatrix}。

从列的角度，这是两个向量的线性组合，找到合适的x、y，使得x倍的（2, -1）加上y倍的（-1, 2），得到（0, 3）。

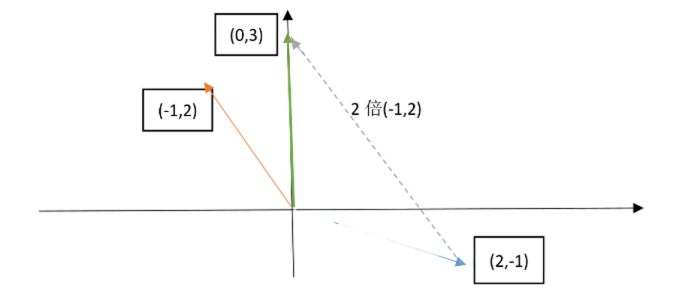
进一步的，如何任意取x、y，将会得到整个平面上任意的向量。

2 方程组的几何解释推广

考虑三元一次方程组：

2.1 高维行图像

按行将方程写成矩阵形式：

其中：

A= \begin{bmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -3 & 4 \\ \end{bmatrix} ， x= \begin{bmatrix} x \\ y \\ z \end{bmatrix} ， b= \begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix} ， 即 Ax=b

从行的角度看，这是三个平面，相交于一点即为解。

直接找到三个平面的交点比较困难，一个可行的方法是，先找出其中两个平面的相交的直线，再找到这条直线与另一个平面的交点。对于更高维度的方程，很难绘制出其图像，求解将变得愈发困难。

2.2 高维列图像

按列将方程写成线性组合：

此时问题转化成，将向量\begin{bmatrix} 2 \\ -1 \\ 0 \end{bmatrix}与向量\begin{bmatrix} -1 \\ 2 \\ -3 \end{bmatrix}正确组合，使得结果为\begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix}。

从列的角度，这是两个向量的线性组合，找到合适的x、y、z，使得x倍的（2, -1, 0）加上y倍的（-1, 2, -3），加上z倍的（0, -1, 4），得到（0, -1, 4）。

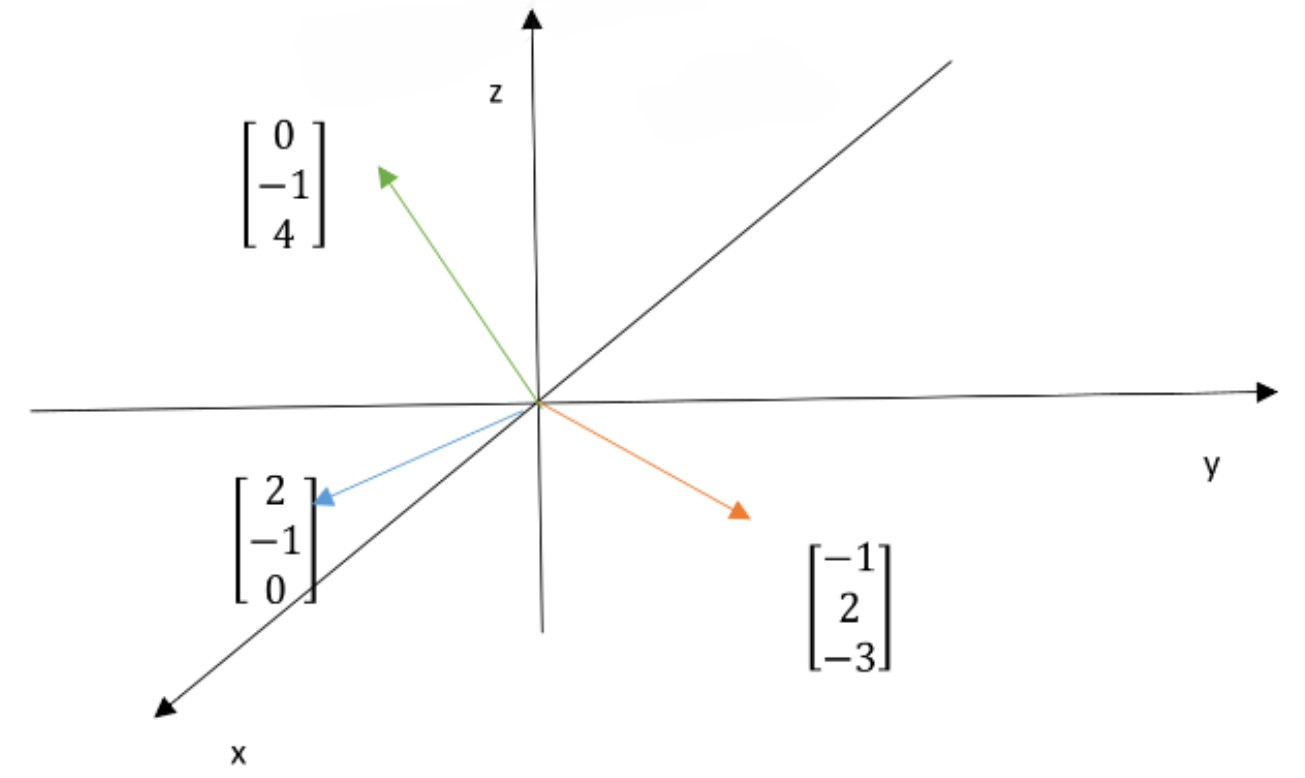
这里很明显能看出解是x=0、y=0、z=1，当然这是一个特例，一眼就能看出答案。列视角把方程看成
x·a₁ + y·a₂ + z·a₃ = b，一次线性组合就给出通解；如果 b 变了，只要再算一组系数即可。行视角却要重画三个平面，逐张找交线，既费时又难在高维里“一眼”定位。
因此，列图像是一种更系统、可扩展的解法。

2.3 方程组是否有解

对于任意b，Ax=b是否都能求解x呢？

以三维为例，如果A的三个向量在同一个平面上，无论他们如何组合，也只能覆盖一个平面，而不是整个三维空间，这种情况下对于任意b，Ax=b可能不能求解x。

2.4 矩阵乘法

A= \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} , x= \begin{bmatrix} 1 \\ 2 \end{bmatrix}，求 Ax。

方法一：

将A看作行向量的组合。

方法二：

将A看作列向量的组合。