1 树的基本概念

节点 (Node)：树的基本组成部分，每个节点存储数据和指向其他节点的链接。图中的每个方框都是一个节点。
根节点 (Root)：树的顶端节点，没有父节点。一棵树只有一个根。
父节点 (Parent) & 子节点 (Child)：一个节点指向的节点是它的子节点，指向它的节点是它的父节点。
边 (Edge)：连接两个节点的线。
叶子节点 (Leaf)：没有子节点的节点，也叫终端节点。
子树 (Subtree)：任何一个节点及其所有后代节点组成的结构，本身也是一棵树。
深度 (Depth)：从根节点到该节点所经过的边的数量。根的深度为 0。
高度 (Height)：从该节点到最远的叶子节点所经过的边的数量。所有叶子节点的高度为 0。树的高度等于根节点的高度。

2 二叉树 & 二叉搜索树 (BST)

2.1 二叉树 (Binary Tree)

这是一种特殊的树，其中每个节点最多有两个子节点，通常称为左子节点和右子节点。

二叉树的遍历（Traversal）：

1 深度优先遍历 (DFS - Depth-First Search)

中序遍历 (In-order)

顺序：左子树 -> 根节点 -> 右子树
结果：对 BST 进行中序遍历，会得到一个升序排列的序列。极其有用！

先序遍历 (Pre-order)

顺序：根节点 -> 左子树 -> 右子树
应用：可用于复制一棵树的结构。

后序遍历 (Post-order)

顺序：左子树 -> 右子树 -> 根节点
应用：常用于删除树节点（先删除子节点再删父节点）或计算目录大小。

2 广度优先遍历 (BFS - Breadth-First Search) （层序遍历）

层序遍历（Level-order）

实现：通常使用队列 (Queue) 辅助实现。

2.2 二叉搜索树 (Binary Search Tree, BST)

这是一种更特殊的二叉树，它增加了一个关键规则，使得搜索效率极高：

规则：对于树中的任意一个节点，其左子树上所有节点的值都小于该节点的值，其右子树上所有节点的值都大于该节点的值。这个规则使得查找一个值的过程就像二分查找一样。

BST 的操作：

查找：从根开始，目标值比当前节点小就往左走，大就往右走，相等就找到。
插入：类似查找，找到应该放置新节点的位置（一个空子节点位置）然后插入。
删除：稍复杂，需要考虑被删除节点是否有 0、1 或 2 个子节点。

BST 的缺陷：如果插入的数据是有序的（如 1, 2, 3, 4, 5），BST 会退化成一条链表！这时，查找的时间复杂度就从理想的 O(log n) 恶化到了最坏的 O(n)。

接下来用 C++ 代码实现二叉搜索树。

首先来看一下头文件 binary_search_tree.h，包含了 BinarySearchTree 类的声明，类中在 private 部分声明了节点的结构体 Node、根节点 root_、插入、搜索、删除、中序、前序、后序、层序，在 public 部分对外提供了插入、搜索、删除、中序、前序、后序、层序的接口。

#ifndef BINARY_SEARCH_TREE_H_
#define BINARY_SEARCH_TREE_H_

#include <memory>

// A binary search tree implementation using smart pointers.
//
// This class provides basic operations for a binary search tree (BST),
// including insertion, search, deletion and traversal methods. It uses
// std::unique_ptr for automatic memory management, ensuring no memory leaks.
class BinarySearchTree {
 public:
  // Constructs an empty binary search tree.
  BinarySearchTree();

  // Destructor is not needed as unique_ptr automatically handles memory cleanup.

  // Inserts a value into the BST.
  //
  // Args:
  //   value: The integer value to insert.
  void Insert(int value);

  // Searches for a value in the BST.
  //
  // Args:
  //   value: The integer value to search for.
  //
  // Returns:
  //   True if the value is found, false otherwise.
  bool Search(int value) const;

  // Removes a value from the BST.
  //
  // Args:
  //   value: The integer value to remove.
  //
  // Returns:
  //   True if the value was found and removed, false otherwise.
  bool Remove(int value);

  // Performs in-order traversal of the BST.
  //
  // In-order traversal visits nodes in ascending order.
  void InOrder() const;

  // Performs pre-order traversal of the BST.
  //
  // Pre-order traversal visits the root first, then left subtree, then right subtree.
  void PreOrder() const;

  // Performs post-order traversal of the BST.
  //
  // Post-order traversal visits left subtree first, then right subtree, then root.
  void PostOrder() const;

  // Performs level-order traversal of the BST.
  //
  // Level-order traversal visits nodes level by level from top to bottom and left to right.
  void LevelOrder() const;

 private:
  // Internal node structure for the BST.
  struct Node {
    int data;                   // The value stored in the node
    std::unique_ptr<Node> left;  // Pointer to the left child
    std::unique_ptr<Node> right; // Pointer to the right child

    // Constructor for creating a new node with the given value.
    //
    // Args:
    //   value: The integer value to store in the node.
    explicit Node(int value);
  };

  std::unique_ptr<Node> root_;  // Root node of the BST

  // Recursively inserts a value into the BST.
  //
  // Args:
  //   node: Reference to a unique_ptr pointing to the current node.
  //   value: The integer value to insert.
  void Insert(std::unique_ptr<Node>& node, int value);

  // Recursively searches for a value in the BST.
  //
  // Args:
  //   node: Reference to a unique_ptr pointing to the current node.
  //   value: The integer value to search for.
  //
  // Returns:
  //   True if the value is found, false otherwise.
  bool Search(const std::unique_ptr<Node>& node, int value) const;

  // Finds the minimum value in a subtree.
  //
  // Args:
  //   node: Pointer to the root of the subtree.
  //
  // Returns:
  //   The node containing the minimum value in the subtree.
  Node* FindMin(Node* node) const;

  // Recursively removes a value from the BST.
  //
  // Args:
  //   node: Reference to a unique_ptr pointing to the current node.
  //   value: The integer value to remove.
  //
  // Returns:
  //   True if the value was found and removed, false otherwise.
  bool Remove(std::unique_ptr<Node>& node, int value);

  // Recursively performs in-order traversal.
  //
  // Args:
  //   node: Reference to a unique_ptr pointing to the current node.
  void InOrder(const std::unique_ptr<Node>& node) const;

  // Recursively performs pre-order traversal.
  //
  // Args:
  //   node: Reference to a unique_ptr pointing to the current node.
  void PreOrder(const std::unique_ptr<Node>& node) const;

  // Recursively performs post-order traversal.
  //
  // Args:
  //   node: Reference to a unique_ptr pointing to the current node.
  void PostOrder(const std::unique_ptr<Node>& node) const;

  // Performs level-order traversal.
  //
  // Args:
  //   node: Reference to a unique_ptr pointing to the root node.
  void LevelOrder(const std::unique_ptr<Node>& root) const;
};

#endif  // BINARY_SEARCH_TREE_H_

接下来看源文件 binary_search_tree.cc，包含了上述类和方法的具体实现。

比较复杂的是节点的删除操作，需要考虑待删除节点如果有 0、1、2 个子节点的情况。

#include "binary_search_tree.h"
#include <iostream>
#include <queue>

// Node constructor implementation
BinarySearchTree::Node::Node(int value) 
    : data(value), left(nullptr), right(nullptr) {}

// BinarySearchTree constructor implementation
BinarySearchTree::BinarySearchTree() : root_(nullptr) {}

// Public Insert method
void BinarySearchTree::Insert(int value) {
  Insert(root_, value);
}

// Private recursive Insert method
void BinarySearchTree::Insert(std::unique_ptr<Node>& node, int value) {
  if (node == nullptr) {
    node = std::make_unique<Node>(value);
  } else if (value < node->data) {
    Insert(node->left, value);
  } else if (value > node->data) {
    Insert(node->right, value);
  }
  // If value == node->data, do nothing (no duplicates allowed)
}

// Public Search method
bool BinarySearchTree::Search(int value) const {
  return Search(root_, value);
}

// Private recursive Search method
bool BinarySearchTree::Search(const std::unique_ptr<Node>& node, int value) const {
  if (node == nullptr) return false;
  if (value == node->data) return true;
  if (value < node->data) return Search(node->left, value);
  return Search(node->right, value);
}

// Public Remove method
bool BinarySearchTree::Remove(int value) {
  return Remove(root_, value);
}

// Private recursive Remove method
bool BinarySearchTree::Remove(std::unique_ptr<Node>& node, int value) {
  if (node == nullptr) return false;  // Value not found

  if (value < node->data) {
    return Remove(node->left, value);
  } else if (value > node->data) {
    return Remove(node->right, value);
  } else {
    // Node to delete found
    if (node->left == nullptr && node->right == nullptr) {
      // Case 1: No children
      node.reset();
    } else if (node->left == nullptr) {
      // Case 2: Only right child
      node = std::move(node->right);
    } else if (node->right == nullptr) {
      // Case 3: Only left child
      node = std::move(node->left);
    } else {
      // Case 4: Two children
      Node* min_node = FindMin(node->right.get());
      node->data = min_node->data;
      Remove(node->right, min_node->data);
    }
    return true;
  }
}

// FindMin method implementation
BinarySearchTree::Node* BinarySearchTree::FindMin(Node* node) const {
  while (node->left != nullptr) {
    node = node->left.get();
  }
  return node;
}

// Public InOrder method
void BinarySearchTree::InOrder() const {
  InOrder(root_);
  std::cout << std::endl;
}

// Private recursive InOrder method
void BinarySearchTree::InOrder(const std::unique_ptr<Node>& node) const {
  if (node == nullptr) return;
  InOrder(node->left);
  std::cout << node->data << " ";
  InOrder(node->right);
}

// Public PreOrder method
void BinarySearchTree::PreOrder() const {
  PreOrder(root_);
  std::cout << std::endl;
}

// Private recursive PreOrder method
void BinarySearchTree::PreOrder(const std::unique_ptr<Node>& node) const {
  if (node == nullptr) return;
  std::cout << node->data << " ";
  PreOrder(node->left);
  PreOrder(node->right);
}

// Public PostOrder method
void BinarySearchTree::PostOrder() const {
  PostOrder(root_);
  std::cout << std::endl;
}

// Private recursive PostOrder method
void BinarySearchTree::PostOrder(const std::unique_ptr<Node>& node) const {
  if (node == nullptr) return;
  PostOrder(node->left);
  PostOrder(node->right);
  std::cout << node->data << " ";
}

// Public LevelOrder method
void BinarySearchTree::LevelOrder() const {
  LevelOrder(root_);
  std::cout << std::endl;
}

// Private LevelOrder method
void BinarySearchTree::LevelOrder(const std::unique_ptr<Node>& root) const {
  if (root == nullptr) {
    std::cout << "Tree is empty" << std::endl;
    return;
  }

  // 使用裸指针队列进行层序遍历是安全的，因为：
  // 1. 遍历期间树的结构不会改变（此函数是const的）
  // 2. 裸指针只在函数局部使用，不影响所有权
  // 3. std::unique_ptr 仍然拥有节点的完整所有权
  std::queue<Node*> node_queue;
  node_queue.push(root.get());
  
  while (!node_queue.empty()) {
    Node* current = node_queue.front();
    node_queue.pop();
    
    std::cout << current->data << " ";
    
    if (current->left != nullptr) {
      node_queue.push(current->left.get());
    }
    if (current->right != nullptr) {
      node_queue.push(current->right.get());
    }
  }
}

最后看 main.cc，编译运行查看测试效果。

#include "binary_search_tree.h"
#include <iostream>


int main() {
  BinarySearchTree bst;
  
  // Insert some values
  bst.Insert(50);
  bst.Insert(30);
  bst.Insert(70);
  bst.Insert(20);
  bst.Insert(40);
  bst.Insert(60);
  bst.Insert(80);
  
  // Perform traversals
  std::cout << "In-order traversal: ";
  bst.InOrder();
  
  std::cout << "Pre-order traversal: ";
  bst.PreOrder();
  
  std::cout << "Post-order traversal: ";
  bst.PostOrder();
  
  std::cout << "Level-order traversal: ";
  bst.LevelOrder();
  
  // Search for values
  std::cout << "Search for 40: " << (bst.Search(40) ? "Found" : "Not found") << std::endl;
  std::cout << "Search for 90: " << (bst.Search(90) ? "Found" : "Not found") << std::endl;
  
  // Remove a value
  std::cout << "Removing 20: " << (bst.Remove(20) ? "Success" : "Not found") << std::endl;
  std::cout << "In-order traversal after removal: ";
  bst.InOrder();
  
  return 0;
}

g++ binary_search_tree.cc main.cc -o main
./main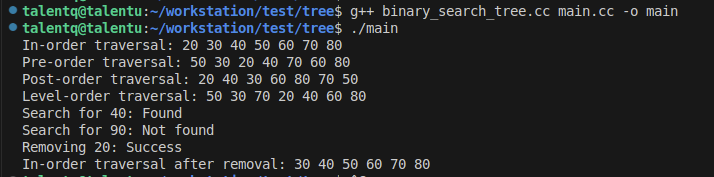

3 平衡二叉树：AVL树和红黑树

为了解决 BST 可能退化的问题，引入了自平衡二叉搜索树。它们通过在插入和删除时进行自动调整（旋转），来保持树的高度大致为 O(log n)。两种最重要的平衡树：AVL树、红黑树

3.1 AVL 树

AVL树是一种高度平衡的二叉搜索树，它通过维护一个平衡因子来确保树的平衡。平衡因子 = 左子树高度 - 右子树高度。对于任何节点，其左子树和右子树的高度差（平衡因子）绝对值不超过 1。

查找性能极高：由于严格平衡，查找时间复杂度稳定在O(log n)
插入/删除代价高：可能需要多次旋转来维持平衡
适合读多写少的场景：如数据库索引、字典等

当插入或删除操作导致平衡因子超出范围时，需要通过旋转来恢复平衡：

左旋 (Left Rotation)：用于处理右子树过高的情况
右旋 (Right Rotation)：用于处理左子树过高的情况
左右旋 (Left-Right Rotation)：先左旋后右旋
右左旋 (Right-Left Rotation)：先右旋后左旋

3.2 红黑树

红黑树是一种大致平衡的二叉搜索树。通过五个规则来确保没有路径会比其他路径长出两倍。它是 C++ STL 中 std::map, std::set, std::multimap, std::multiset 的底层实现容器。

特点：它不是高度平衡的，但可以保证从根到叶子的最长路径不会超过最短路径的两倍。这是一种折中，虽然查找比 AVL 稍慢，但插入和删除的效率更高，需要的旋转操作更少。

特点：

插入/删除性能好：相比AVL树，需要的旋转操作更少
查找性能稍差：没有AVL树那么平衡，但仍是O(log n)
综合性能均衡：适合频繁插入删除的场景

五条规则：

每个节点是红色或黑色
根节点是黑色
所有叶子节点（NIL）是黑色
红色节点的子节点必须是黑色（不能有连续红色节点）
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

当插入或删除违反规则时，通过以下操作恢复平衡：

变色 (Recoloring)：改变节点颜色
旋转 (Rotation)：与 AVL 树类似的旋转操作

3.3 为什么 C++ STL 选择红黑树

主要是因为STL中的map和set等关联容器需要频繁执行插入和删除操作，而红黑树在整体性能上提供了更好的平衡。它牺牲了少量严格的平衡性来换取更高效的插入和删除效率，这对于STL的通用设计哲学更为重要。

这是一个典型的工程上的权衡（Trade-off）。虽然AVL树在查找上有着理论上的优势，但C++ STL的设计者经过权衡后认为，对于其目标应用场景（需要大量增删改查的通用编程），红黑树在整体性能和实现复杂度上提供了更好的折衷。

在实际硬件上，由于缓存等原因，红黑树较少的旋转操作也带来了更好的性能表现。

4 扩展

如何计算一棵树的高度/最大深度？

int MaxDepth(std::unique_ptr<Node>& node) {
  if (node == nullptr) return 0;
  return std::max(MaxDepth(node->left), MaxDepth(node->right)) + 1;
}

如何判断两颗二叉树是否相同？

bool IsSameTree(std::unique_ptr<Node>& p, std::unique_ptr<Node>& q) {
  if (p == nullptr && q == nullptr) return true;
  if (p == nullptr || q == nullptr) return false;
  if (p->data != q->data) return false;
  return IsSameTree(p->left, q->left) && IsSameTree(p->right, q->right);
}

如何判断一棵二叉树是否是对称二叉树/镜像对称的？

bool IsISymmetrical(std::unique_ptr<Node>& node) {
  if (node == nullptr) return true;
  std::unique_ptr<Node>& p = node->left;
  std::unique_ptr<Node>& q = node->right;
  return IsISymmetricalPQ(p, q);
}

bool IsISymmetricalPQ(std::unique_ptr<Node>& p, std::unique_ptr<Node>& q) {
  if (p == nullptr && q == nullptr) return true;
  if (p == nullptr || q == nullptr) return false;
  if (p->data != q->data) return false;
  return IsISymmetricalPQ(p->left, q->right) && IsISymmetricalPQ(p->right, q->left);
}

如何使用迭代的方式实现二叉树的前序、中序、后序遍历？

void PreOrderByStack(std::unique_ptr<Node>& root) {
  if (root == nullptr) return;
  std::stack<Node*> s;
  s.push(root.get());
  while (!s.empty()) {
    Node* current = s.top();
    s.pop();
    std::cout << current->data << " ";
    if (current->right != nullptr) s.push(current->right.get());
    if (current->left != nullptr) s.push(current->left.get());
  }
}

void InOrderByStack(std::unique_ptr<Node>& root) {
  if (root == nullptr) return;
  std::stack<Node*> s;
  Node* current = root.get();
  while (current != nullptr || !s.empty())
  {
    while (current != nullptr) {
      s.push(current);
      current = current->left.get();
    }
    current = s.top();
    s.pop();
    std::cout << current->data << " ";
    current = current->right.get();
  }
}

void PostOrderByStack(std::unique_ptr<Node>& root) {

}

C++ STL 中的 map（或 set）底层是如何实现的？它有什么特点？

底层通常是红黑树（一种自平衡二叉搜索树）。

元素是自动排序的（按 key 排序）。
查找、插入、删除操作的时间复杂度都是 O(log n)。
支持高效的区间遍历和范围查询。

对比 unordered_map：unordered_map 底层是哈希表，元素无序，但平均查找时间复杂度是 O(1)。

为什么 std::map 选择红黑树而不是 AVL 树作为底层结构？

虽然 AVL 树更平衡，查找更快（O(log n)），但红黑树在插入和删除操作时需要更少的旋转来维持平衡，整体性能更均衡。对于需要频繁插入删除的通用关联容器（如 std::map），红黑树是更好的选择。

什么是线索二叉树？它有什么用处？

答：在线索二叉树中，所有为 nullptr 的左、右指针被重新利用：如果一个节点的左指针为空，则让它指向其前驱节点；如果右指针为空，则指向其后继节点（这里的“前驱”和“后继”指的是中序遍历序列中的前后关系）。
用处：它使得在不使用栈或递归的情况下进行中序遍历成为可能，并且可以更快地找到前驱和后继节点。它节省了内存空间（不需要为每个节点维护指向父节点的指针），但增加了复杂性。

目录CONTENT

数据结构：树