1 引言：模型训练不起来怎么办

可能是因为梯度为0，导致参数不再更新，模型训练也就停滞不前了。梯度为0有两种情况：

它们被统称为 critical point。

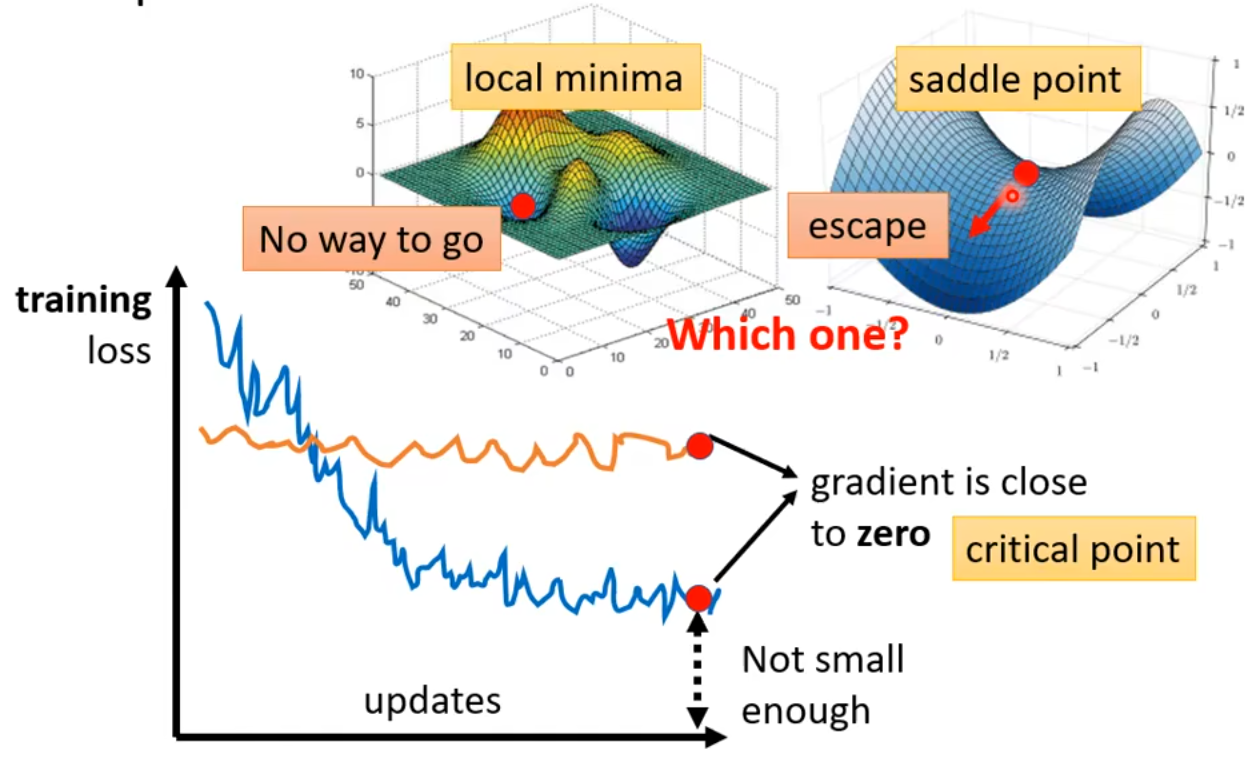
但是怎么知道当遇到critical point的时候，它具体属于哪一类呢？

local minimal无路可逃，saddle point可以逃离。

2 泰勒近似（Tayler Series Approximation）

这一节涉及数学知识，了解原理即可。

我们用一个表达式来近似模型对于参数\boldsymbol \theta的损失L(\boldsymbol \theta)：

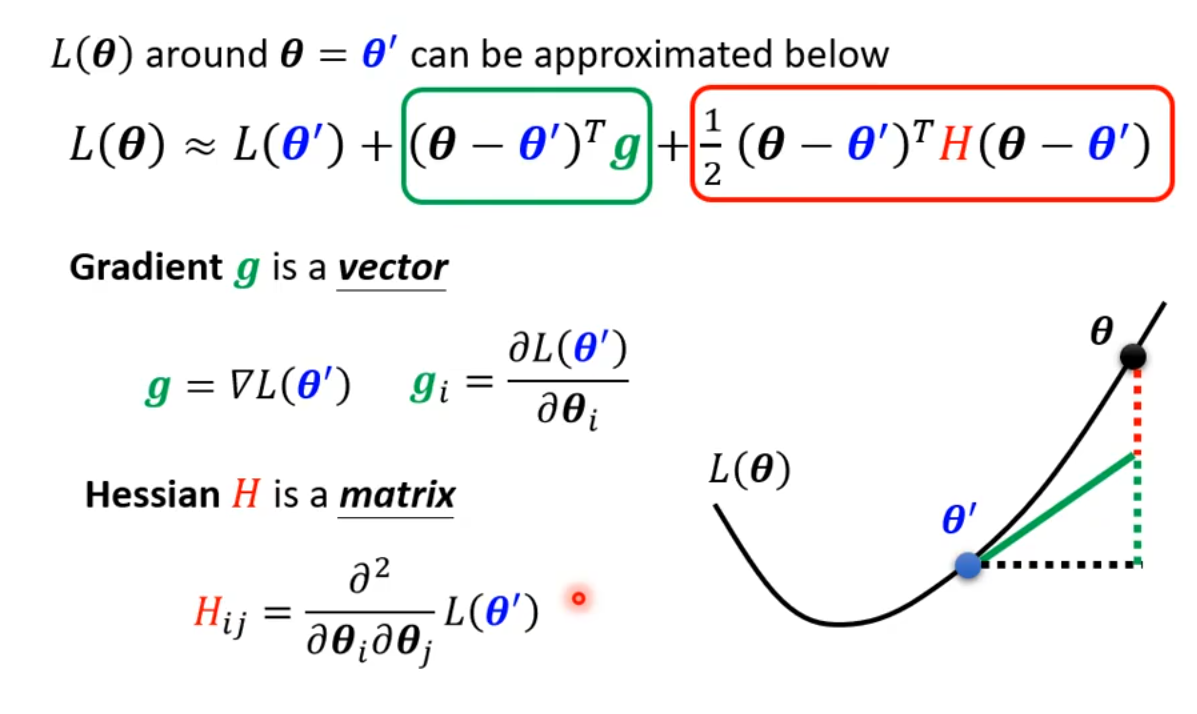
当遇到critical point的时候：

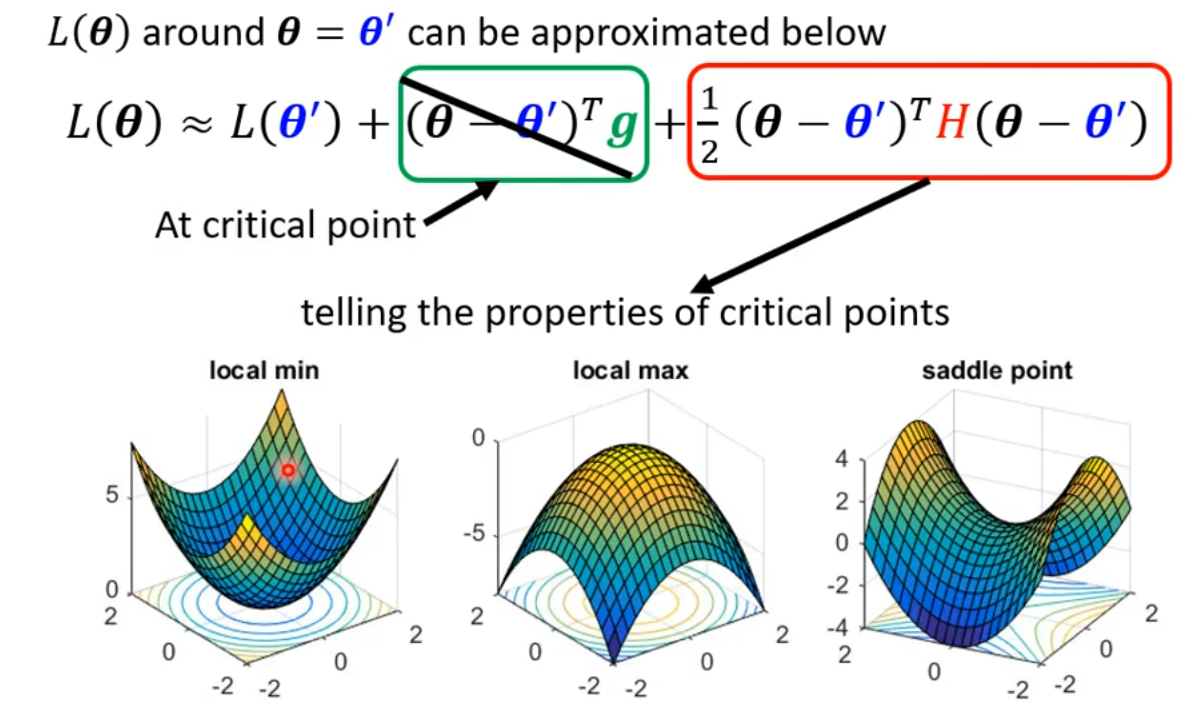
只需要根据Hessian \boldsymbol H判断，其中 eigen value 是特征值：

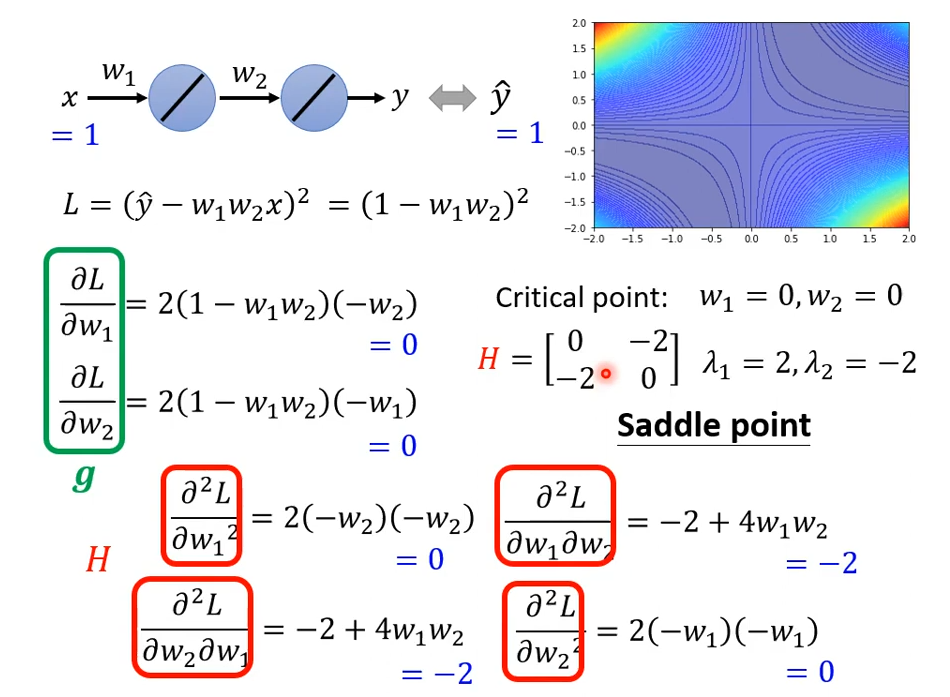
举例子：

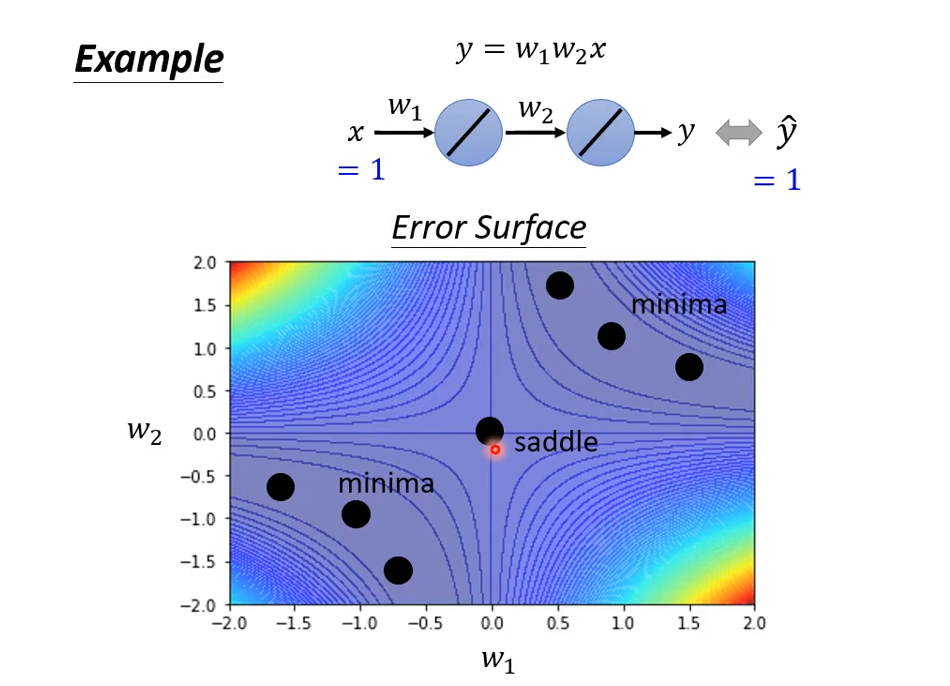
通过计算判断点 (0, 0) 是 saddle point：

如果遇到 saddle point，我们可以通过Hessian \boldsymbol H判断模型参数更新的方向：

举例子：

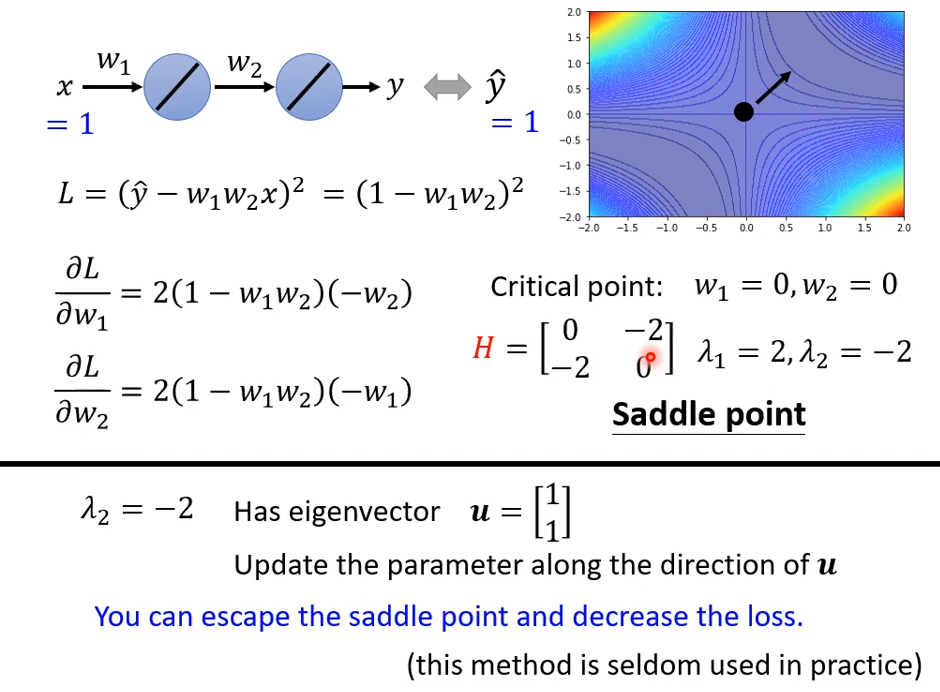
这个Hessian方法在实际中几乎不会使用，因为计算量非常大。这里引出这个方法只是为了说明，遇到 saddle point 也是有解决办法的。还有一些好的解决办法我们以后再学习。

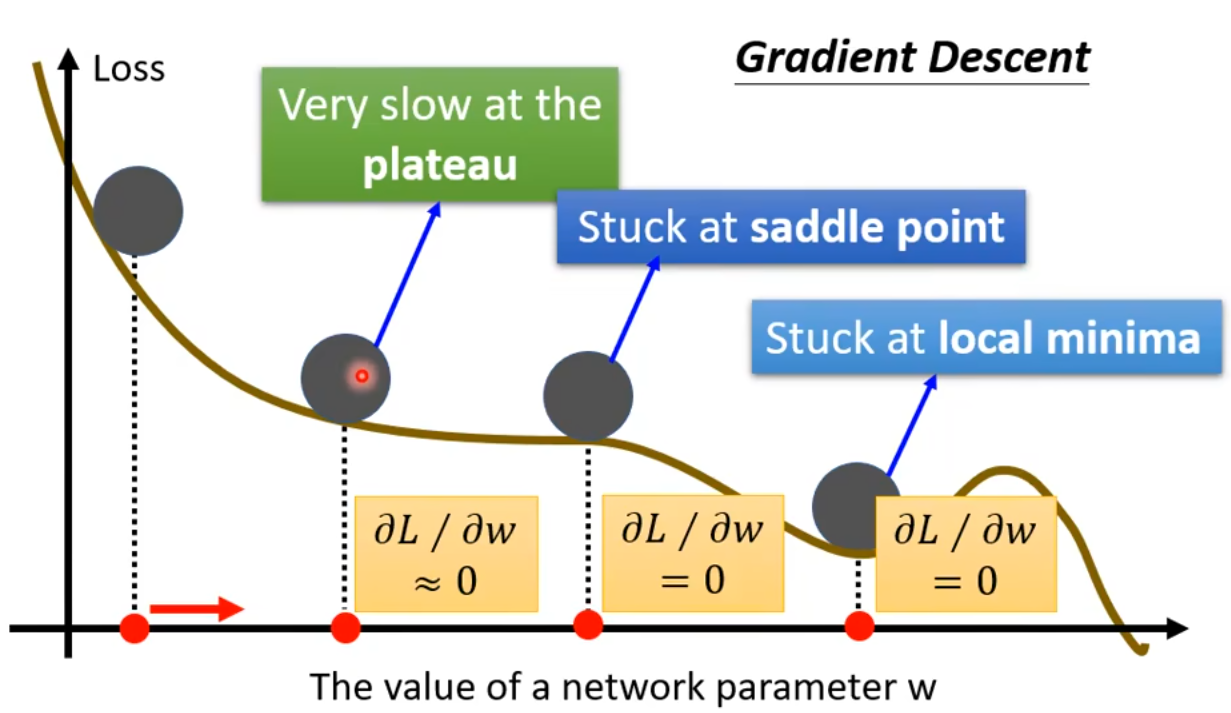
当loss还很大，但是此时梯度变得很小，训练停滞不前时，可能是遇到了非常平坦的地方，可能是local minima，也可能是saddle point。

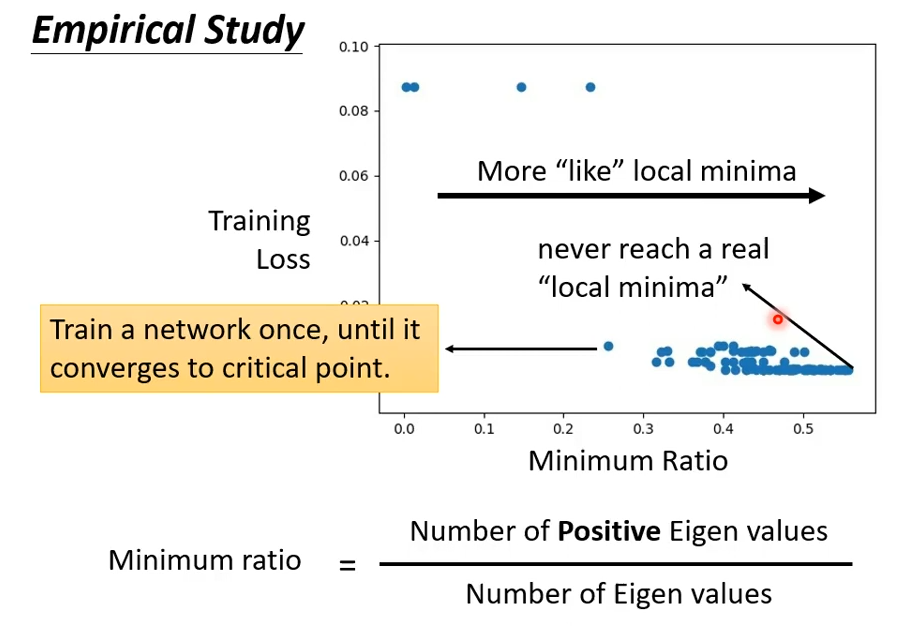
根据经验，当模型参数有很多时，遇到 local minima 的情况是非常罕见的。如果模型的loss很大并且不再下降，基本上都是卡在了 saddle point。