1 Linear Model的局限性
对于线性模型y = b + wx_1,模型训练的过程可以不断更新b和w,但是不论如何变化,该模型始终是一条直线:
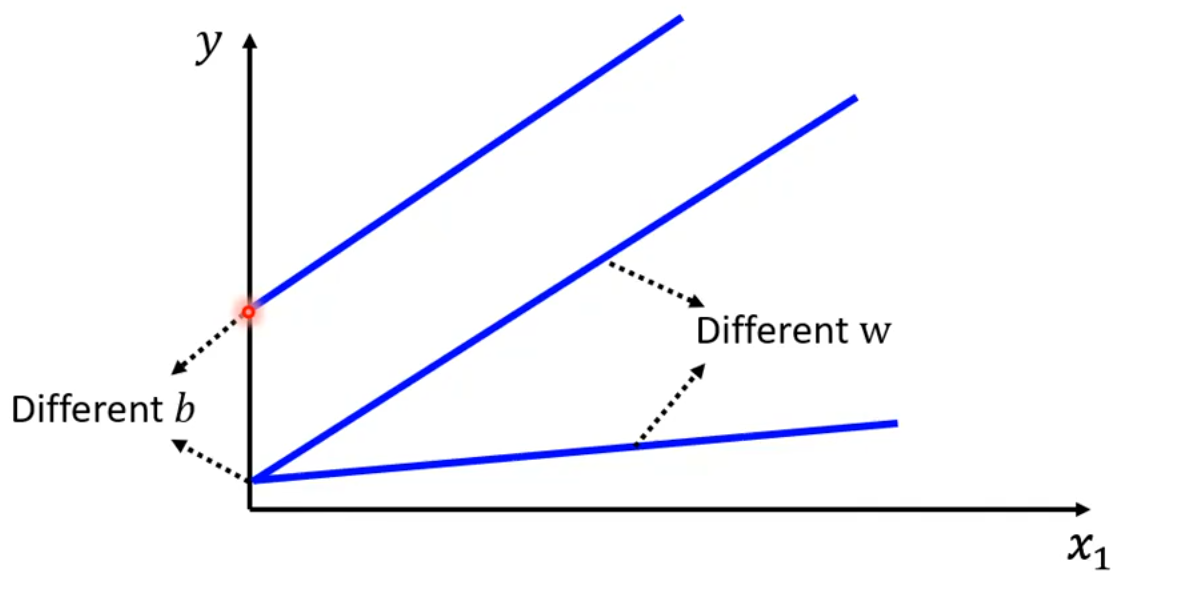
对于训练数据,也许数据满足的是红线的模型。如果是这样,无论我们训练出多么好的线性模型y = b + wx_1,模型的预测能力与真实情况仍存在较大差距。
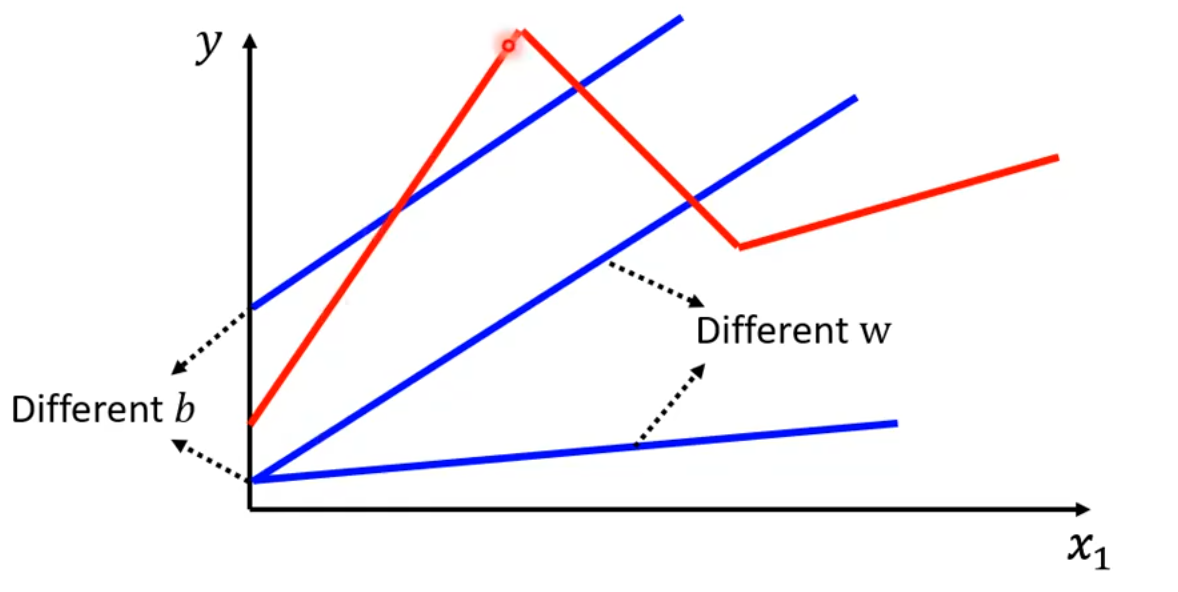
于是我们得出结论:
线性模型存在严重的局限性,称为模型偏差(Model Bias)。
2 探索更复杂的模型
2.1 分段线性曲线(Piecewise Linear Curves)
如果最佳模型曲线如下图中红线所示:
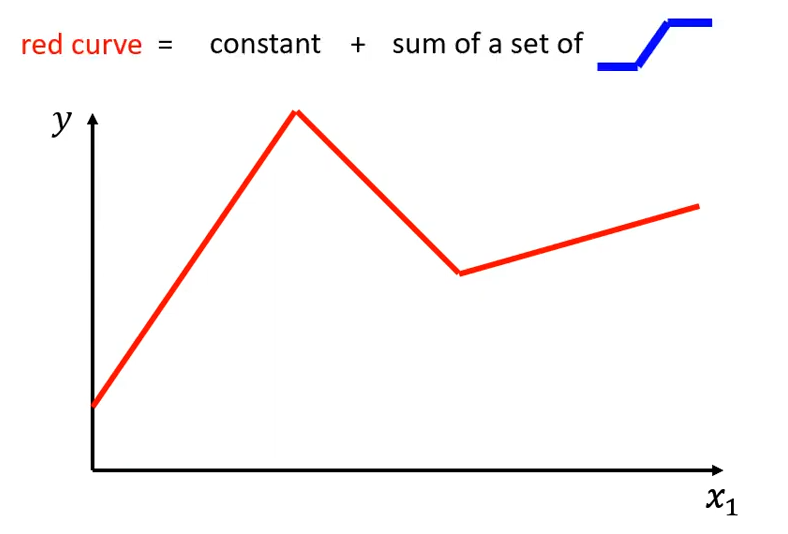
我们该如果写出该模型的的函数呢?首先明确一点,红线 = 常量 + 一系列的蓝线之和。这里的蓝线是一个 “常量-斜线-常量“ 的分段函数。可能不太好理解,接下来做一下解释。
0. 首先是第0条蓝线,表示红线的常量。
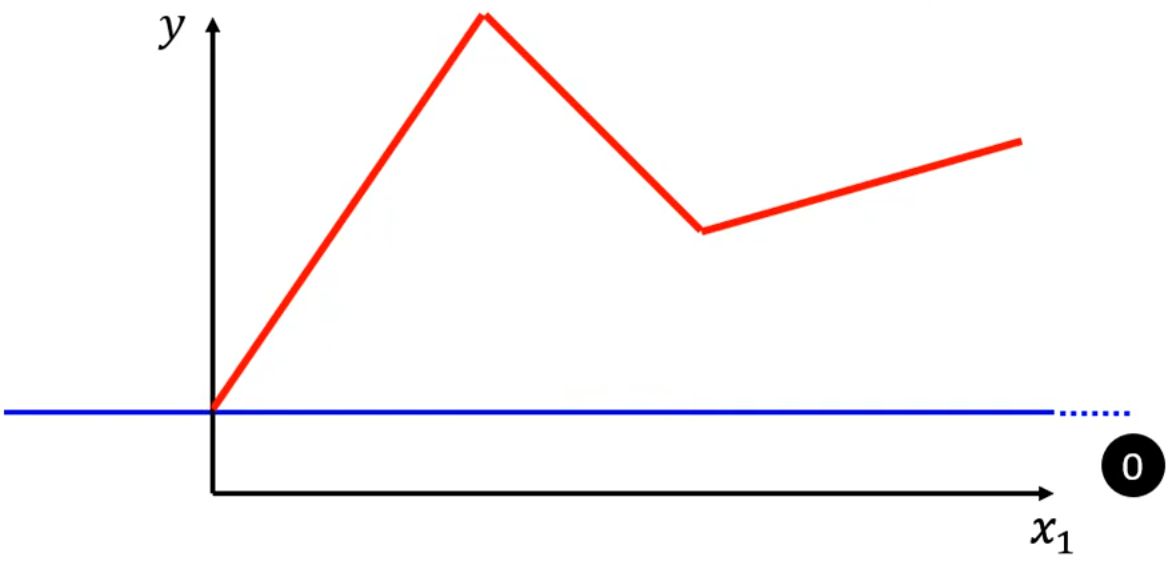
2.1.1 增加第1条蓝线,用于表示红线的第1段。蓝线有以下特征:
当x_1 < 0时恒为常数;
当0 \le x_1 < 红线第一个拐点时,斜率与红线相同;
当x_1 \ge 红线第一个拐点时恒为常数。
此时,第0条蓝线 + 第1条蓝线,就能表示出红线的第一段。
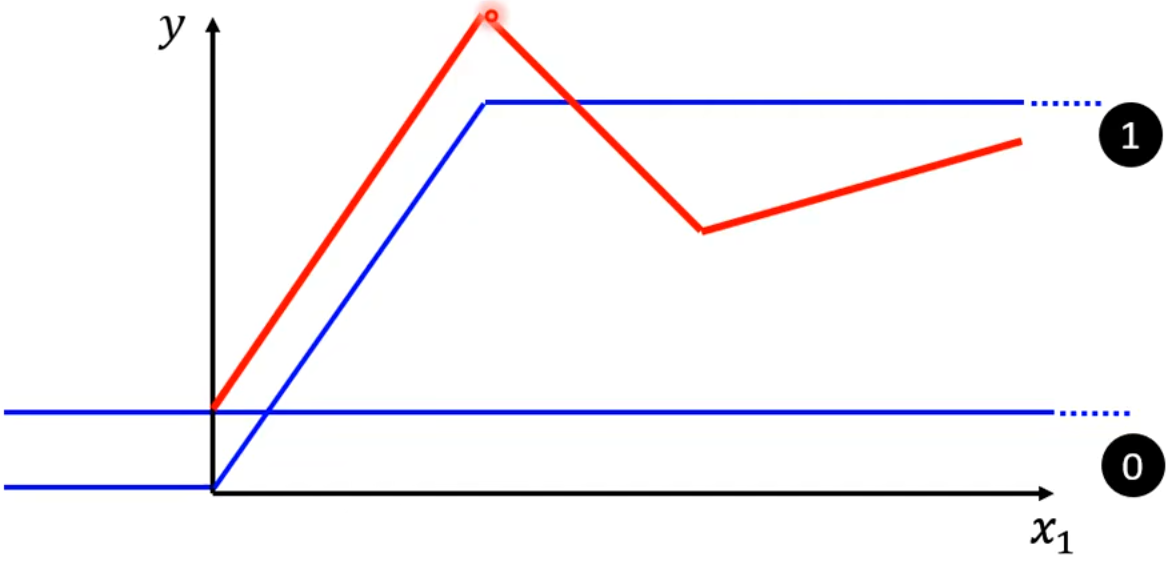
2.1.2 增加第2条蓝线,用于表示红线的第2段。
此时,第0条蓝线 + 第1条蓝线 + 第2条蓝线,就能表示出红线的前两段。
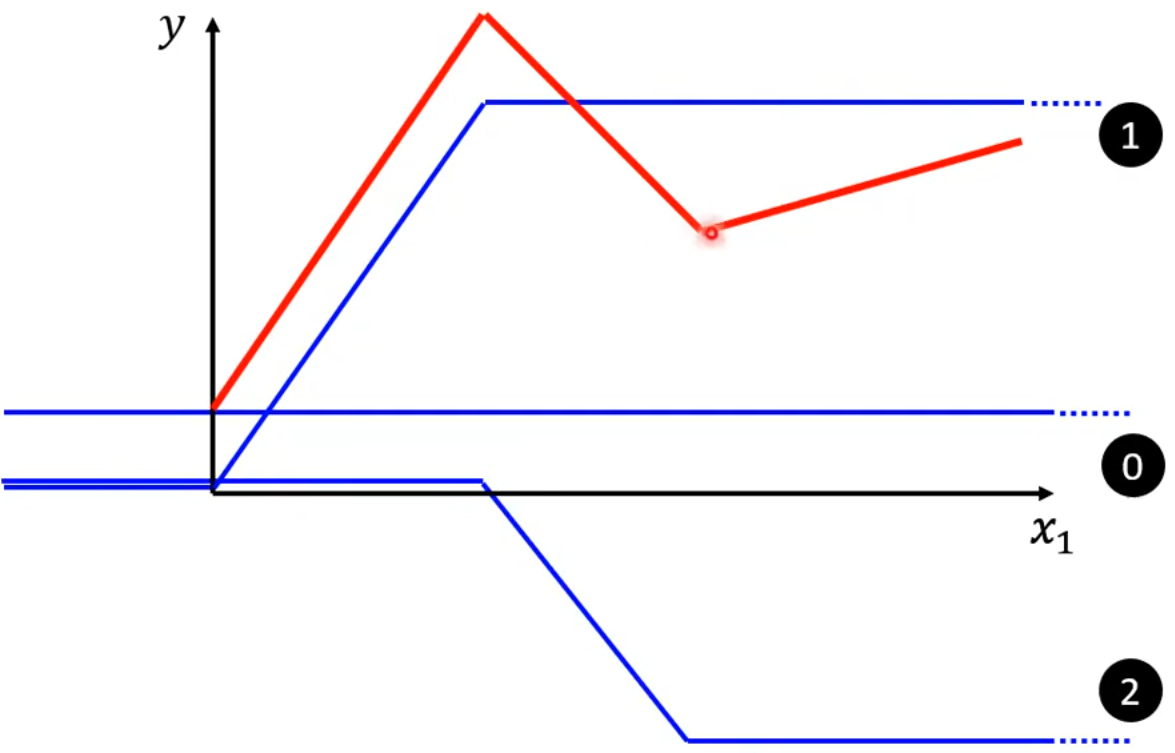
2.1.3 增加第3条蓝线,用于表示红线的第3段。
此时,第0条蓝线 + 第1条蓝线 + 第2条蓝线 + 第3条蓝线,就能表示出红线。
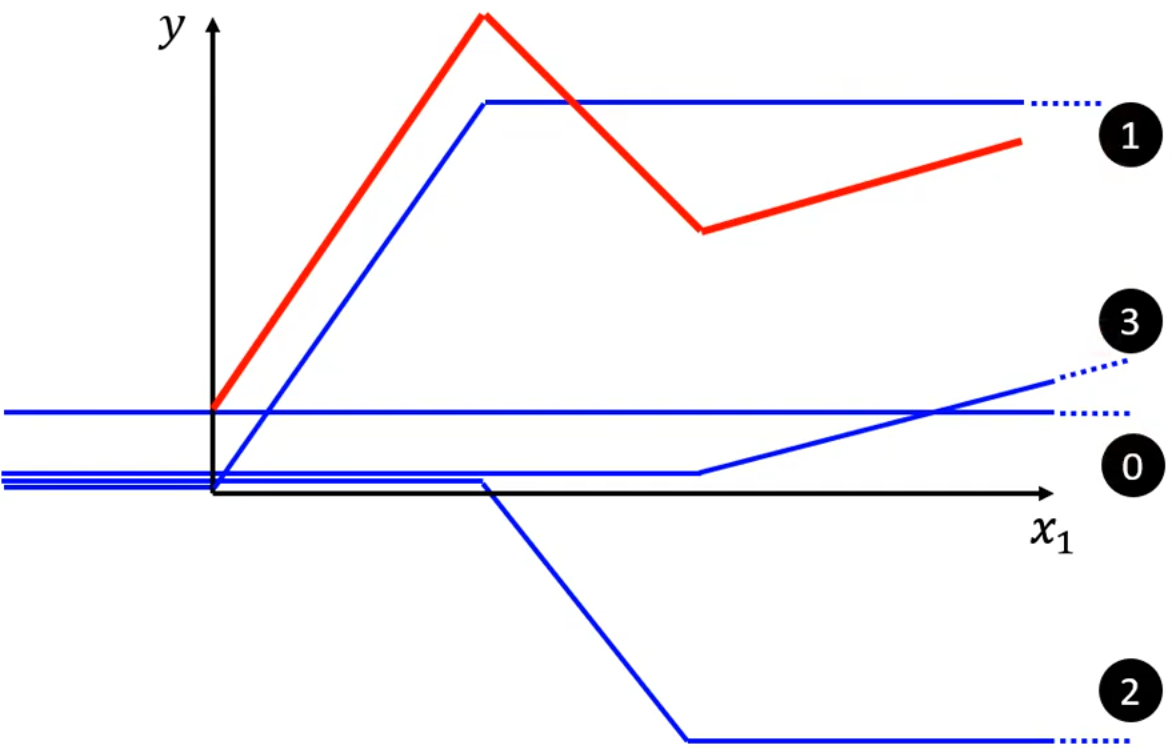
由上述过程我们很容易推导出:
任意分段线性曲线 = constant + 一系列的蓝线之和。
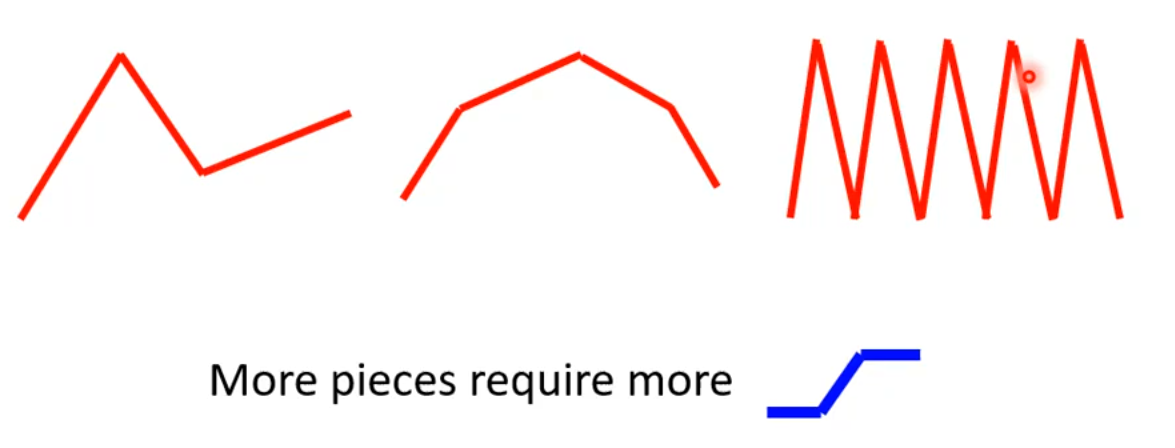
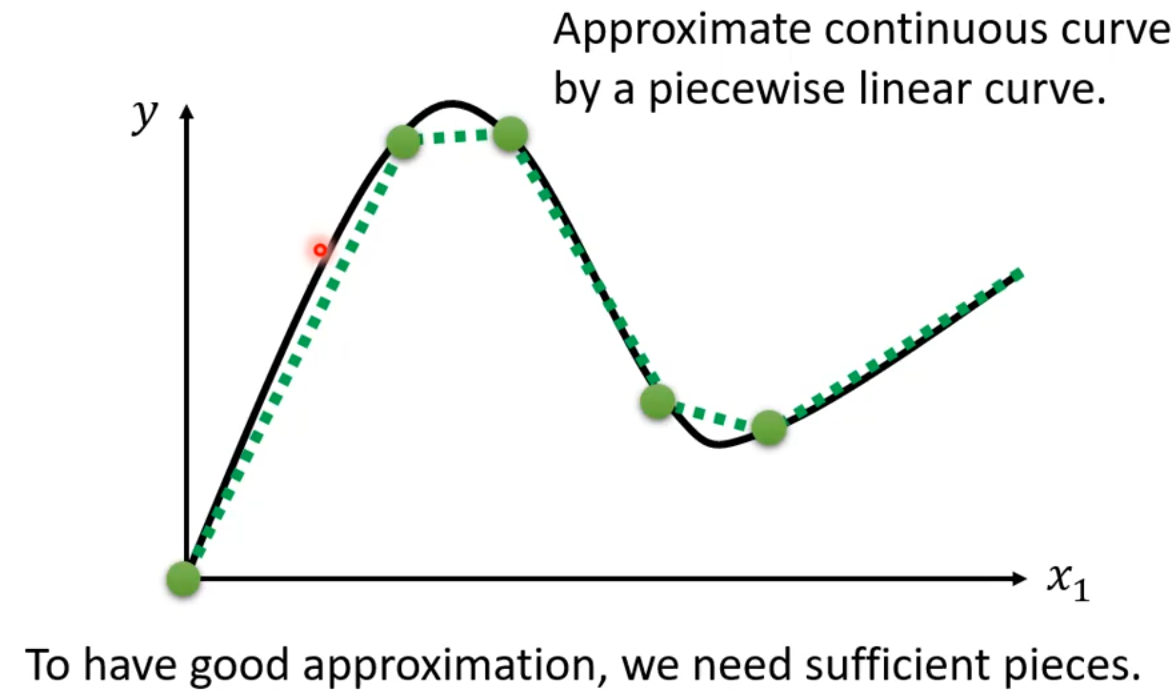
到这里还不够,因为我们经常见到的是平滑的曲线,而不是分段线性曲线,怎么办呢?
对于平滑的曲线,可以在曲线上取很多点连接起来,这样就形成了分段线性曲线。只要取的点足够多,就可以使用分段线性曲线来逼近平滑的曲线。
2.2 Sigmoid Function
上一小节中,多次使用“蓝线”,我们如何用函数去表示它呢?
我们先用Sigmoid函数来近似这个分段函数。(这里不用纠结为什么使用Sigmoid函数)。我们称原来的“蓝线”为 Hard Sigmoid。
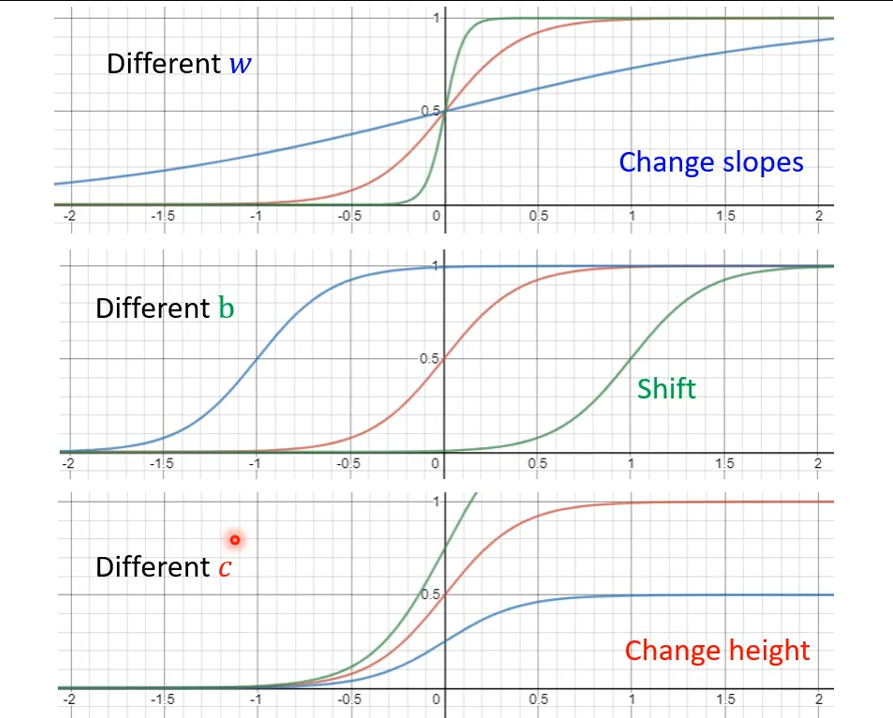
Sigmoid Function,由于其形状像“S”而得名,可以称之为“S函数”。其函数表达式为:
w改变坡度,b改变左右位移,c改变高度:
2.3 更换模型
我们已经用sigmoid函数表示了“蓝线”,接下来就可以写出“红线”的函数了。红线 = 常量 + 一系列的蓝线之和。
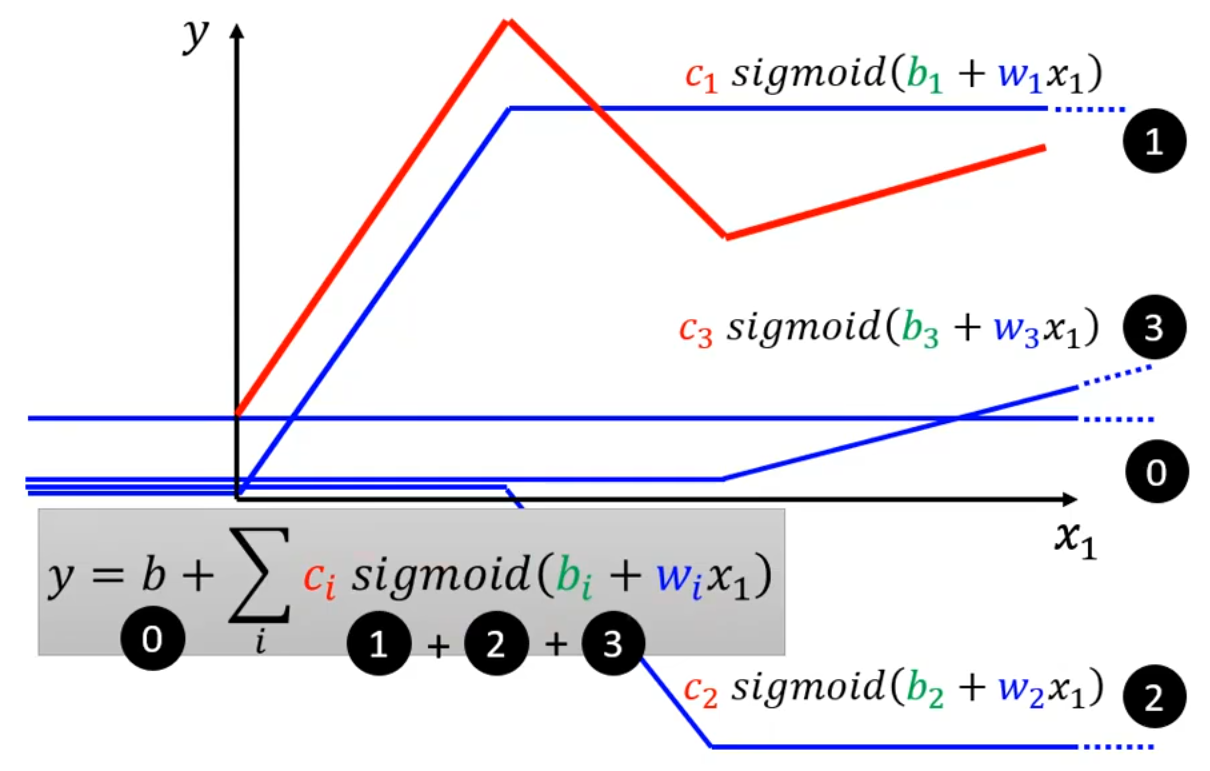
将线性模型y = b + wx_1可以更换成:
其中i表示第几个sigmoid函数。
将线性模型y = b + \sum_j w_jx_j可以更换成:
其中i表示第几个sigmoid函数,j表示第几个feature(即后一天的数据与前多个天的数据相关)。
3 写出带有未知参数的Function
实际上我们已经写出了这个Function,就是:
这个模型表达式完全OK,就是有点太“算术”了,不够“矩阵”。接下来将以该模型为例,引入矩阵和向量的概念,将模型表达式转换成更抽象但是易于理解和表达的样子。
我们的例子中,考虑i的取值为1、2、3,表示有三个sigmoid函数;j的取值为1、2、3,表示只考虑前三天的数据对后一天数据的影响。这里的i和j的最大值,是可以人为指定的,是超参数。
3.1 sigmoid()函数的参数
3.1.1 我们先探究sigmoid()函数的参数:
下图中,黑色圈圈1、2、3表示i的取值;黄色方块x_1, x_2, x_3表示feature,即前三天的真实数据;黑色连线表示feature要乘以权重w。对于每一个i,都要计算出一个值,记作r_i,即r_1, r_2, r_3,r_i即是sigmoid()函数的参数。
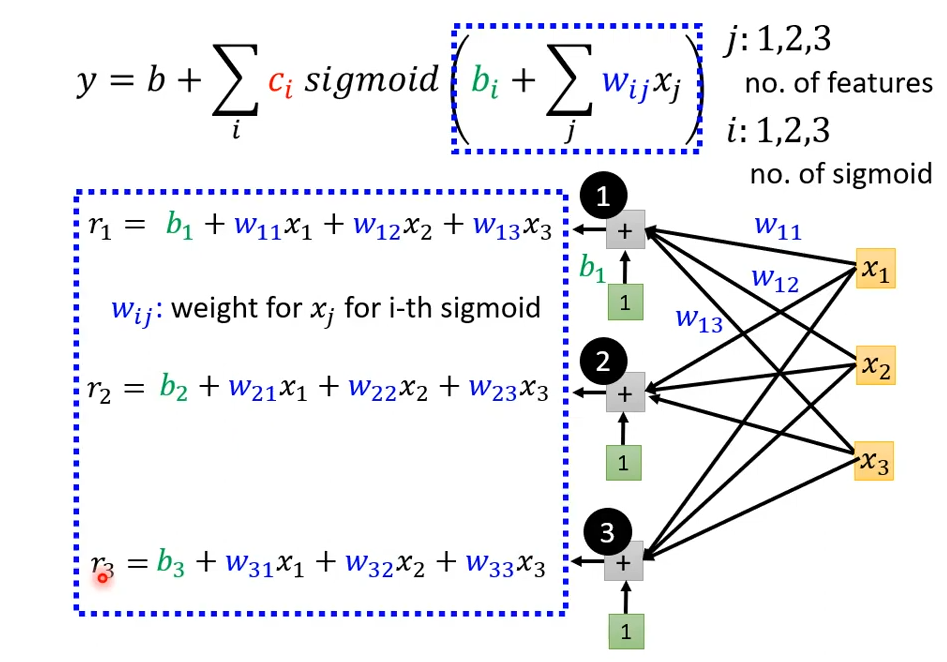
接下来用神奇的转换时刻。将算术式转换成矩阵,再转换成向量。这三种表示方法本质上是一样的,只是写出来的表现形式不同。注意,通常使用加粗的字母表示向量,比如\boldsymbol r。
使用向量的形式表示为:
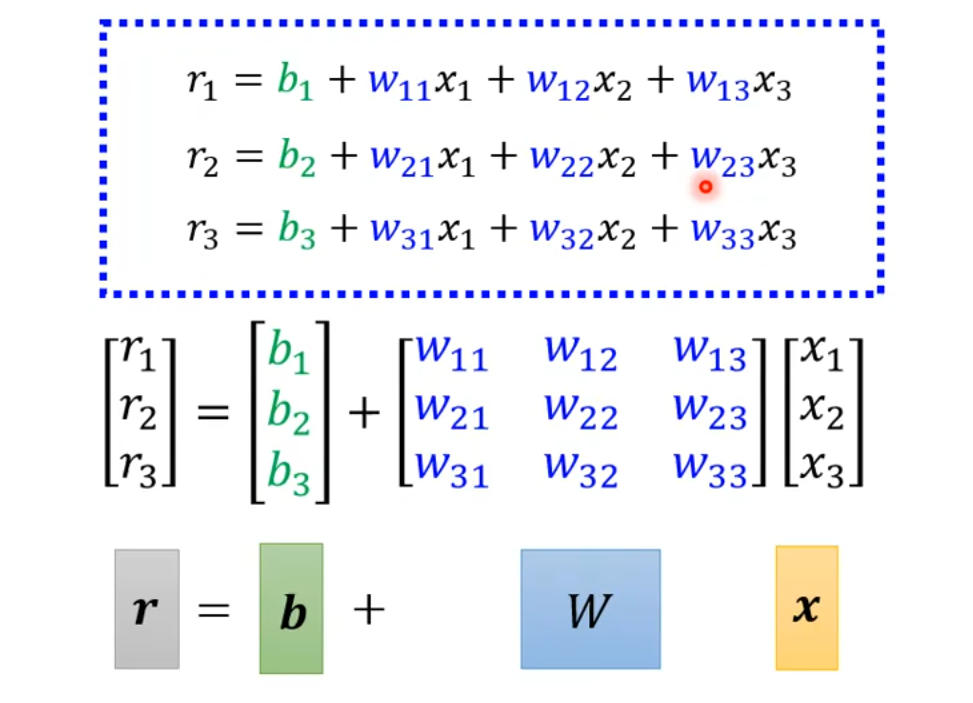
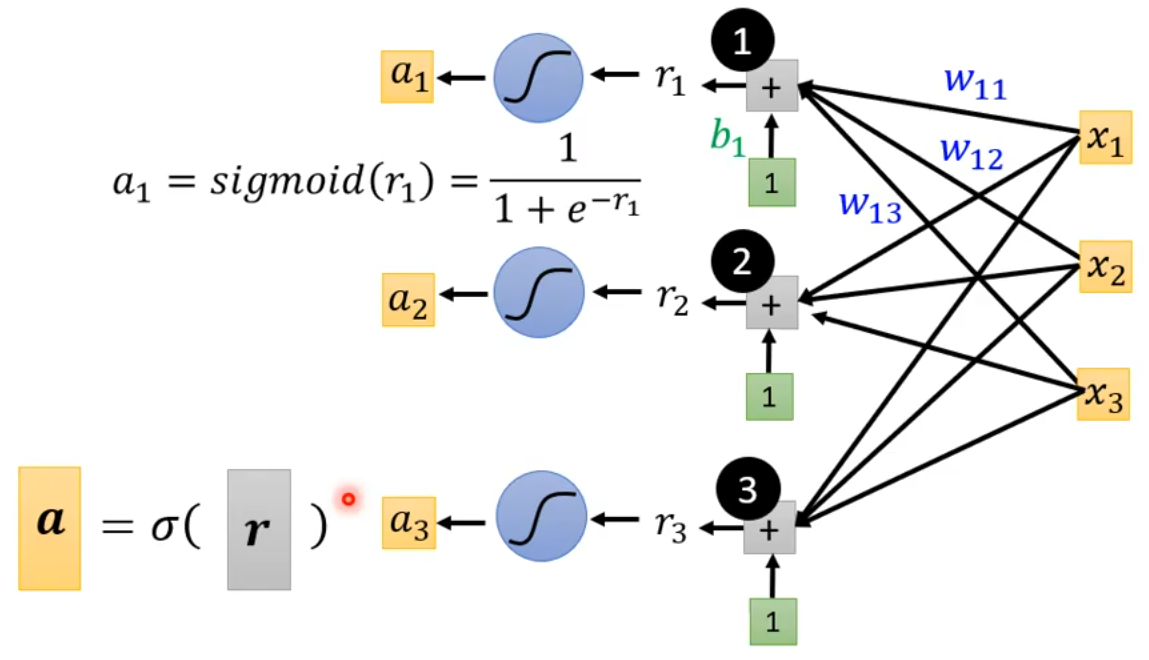
3.1.2 将参数带入sigmoid函数
即将r_i带入sigmoid函数得到a_i。多个a_i可以写成向量\boldsymbol a,即:
3.1.3 写出模型完整的函数
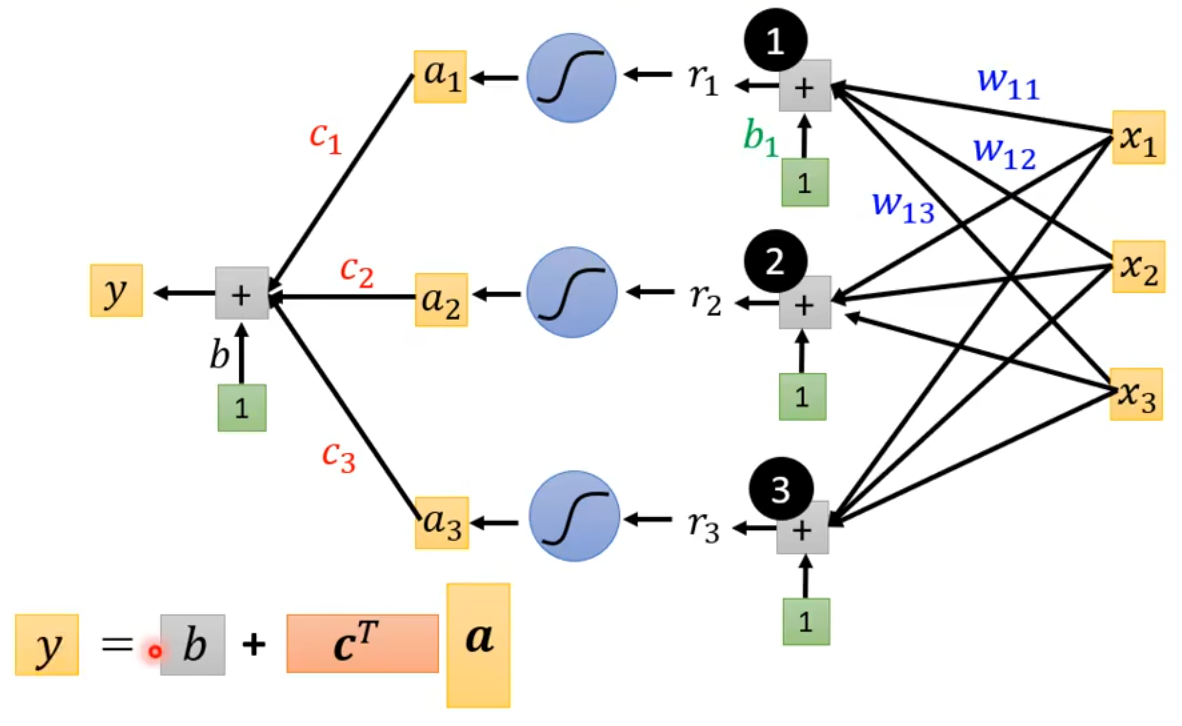
上图中的表达式y = b + \boldsymbol {c^T} \boldsymbol a,其中\boldsymbol c是\begin{bmatrix} c_1 \\ c_2 \\ c_3 \end{bmatrix} ,\boldsymbol {c^T}是\boldsymbol c的转置,即\begin{bmatrix} c_1 & c_2 & c_3 \end{bmatrix}。最终我们得到模型完整的函数为:
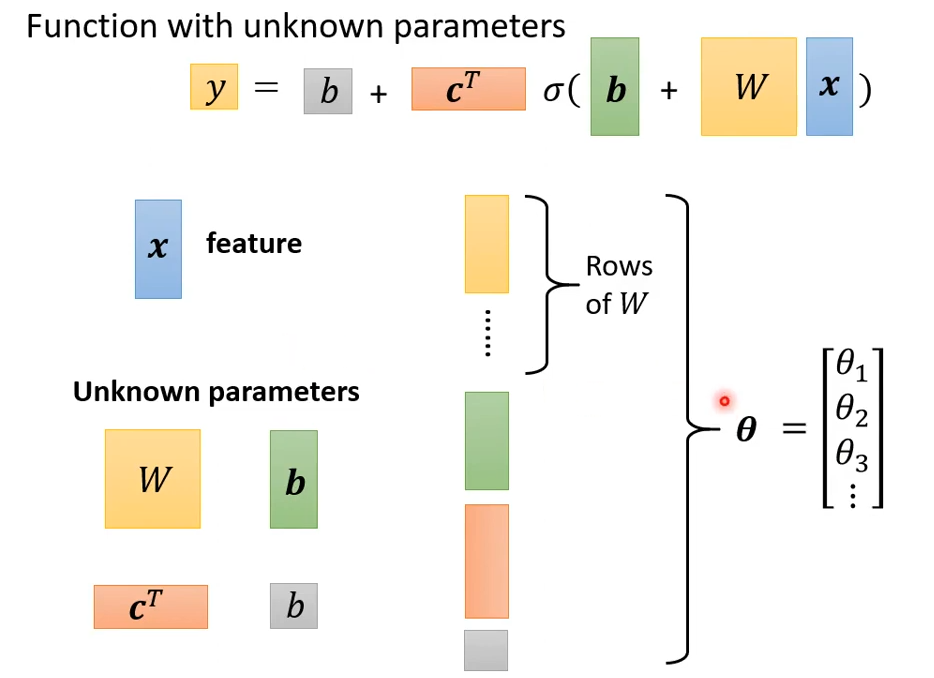
3.1.4 未知参数
向量\boldsymbol x是feature,是已知的数据;向量\boldsymbol W, \boldsymbol b, \boldsymbol c^T和标量b是未知参数。将未知参数连接起来(就是直接从上到下一字排开),用向量\boldsymbol \theta表示,\theta_1, \theta_2, \theta_3 ...是向量\boldsymbol \theta中的一个个元素。
4 定义损失函数(Loss Function)
损失函数是对未知参数的函数,上一小节中我们将所有的未知参数连接在一起形成了向量\boldsymbol \theta,所以此时损失函数是对\boldsymbol \theta的函数L(\boldsymbol \theta)。
损失是用来评估某组未知参数的好坏。
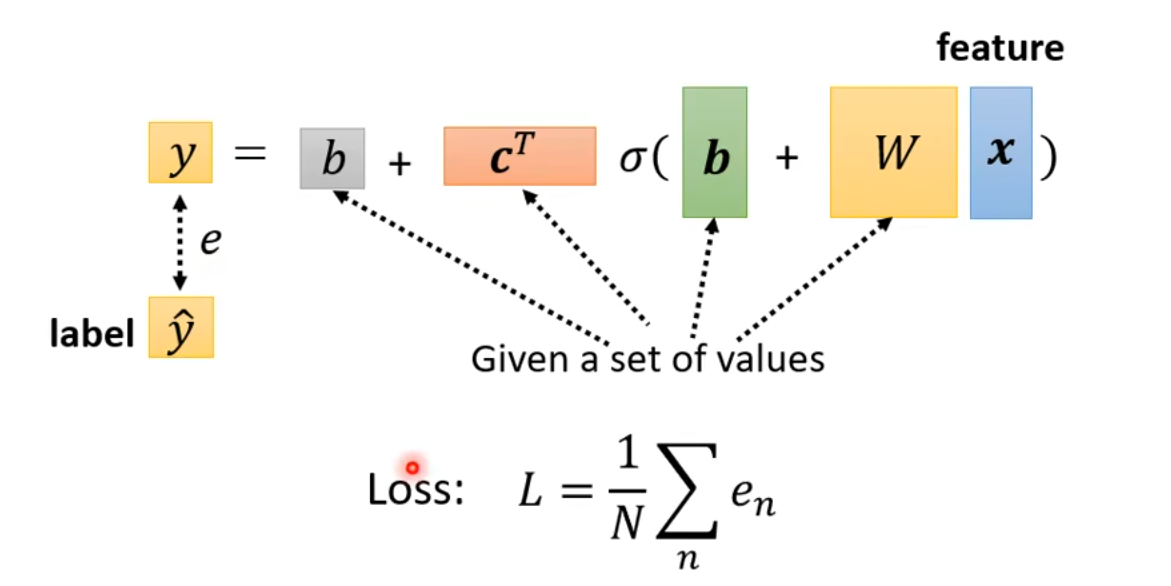
label:真实值,即这里的\^{y};e是y和\^{y}的差值的绝对值。最终的损失函数Loss为:
5 优化(Optimization)
优化是为了找出使损失最小的参数:
1 随机选取一个初始的值\boldsymbol \theta^0;
2 计算梯度(gradient)\boldsymbol g = \bigtriangledown L(\boldsymbol \theta^0);
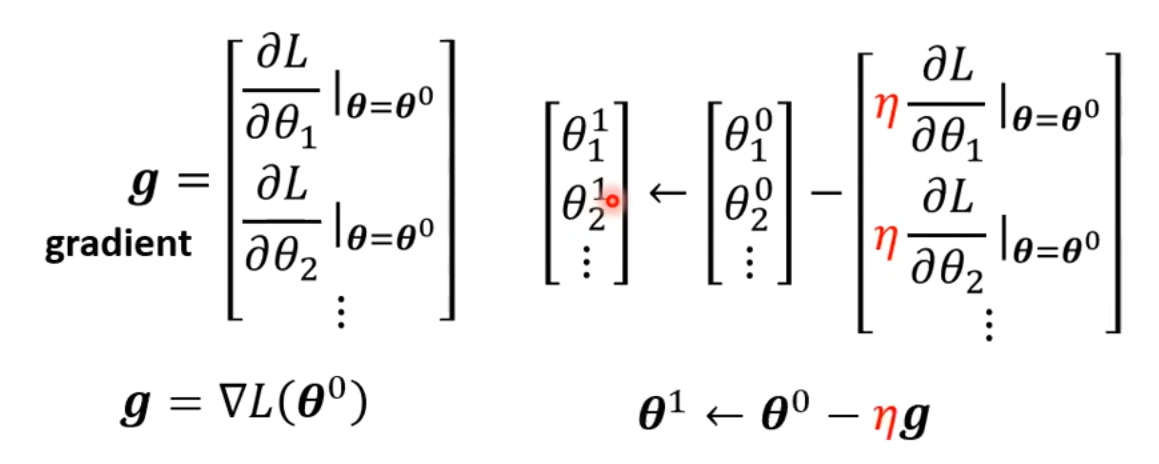
3 更新参数:\boldsymbol \theta^1 \leftarrow \boldsymbol \theta^0 - \eta\ \boldsymbol g;
4 继续计算梯度(gradient):\boldsymbol g = \bigtriangledown L(\boldsymbol \theta^1),:\boldsymbol \theta^2 \leftarrow \boldsymbol \theta^1 - \eta\ \boldsymbol g;直到\boldsymbol g = 0或者达到了指定的最大更新次数。
以上是原理,接下来介绍实际情况下是如何使用梯度下降的。
对于给定的N条数据,将其随机均等分成多个块,每一块称为batch(B)。上文我们讲解梯度下降操作时,每一次计算梯度,都使用全部的N条数据。而实际上应该是,
使用第1个batch的数据计算第1个梯度g = \bigtriangledown L(\boldsymbol \theta^1),并更新参数\boldsymbol \theta^1 \leftarrow \boldsymbol \theta^0 - \eta\ \boldsymbol g;
使用第2个batch的数据计算第2个梯度g = \bigtriangledown L(\boldsymbol \theta^2),并更新参数\boldsymbol \theta^2 \leftarrow \boldsymbol \theta^1 - \eta\ \boldsymbol g;
以此类推。
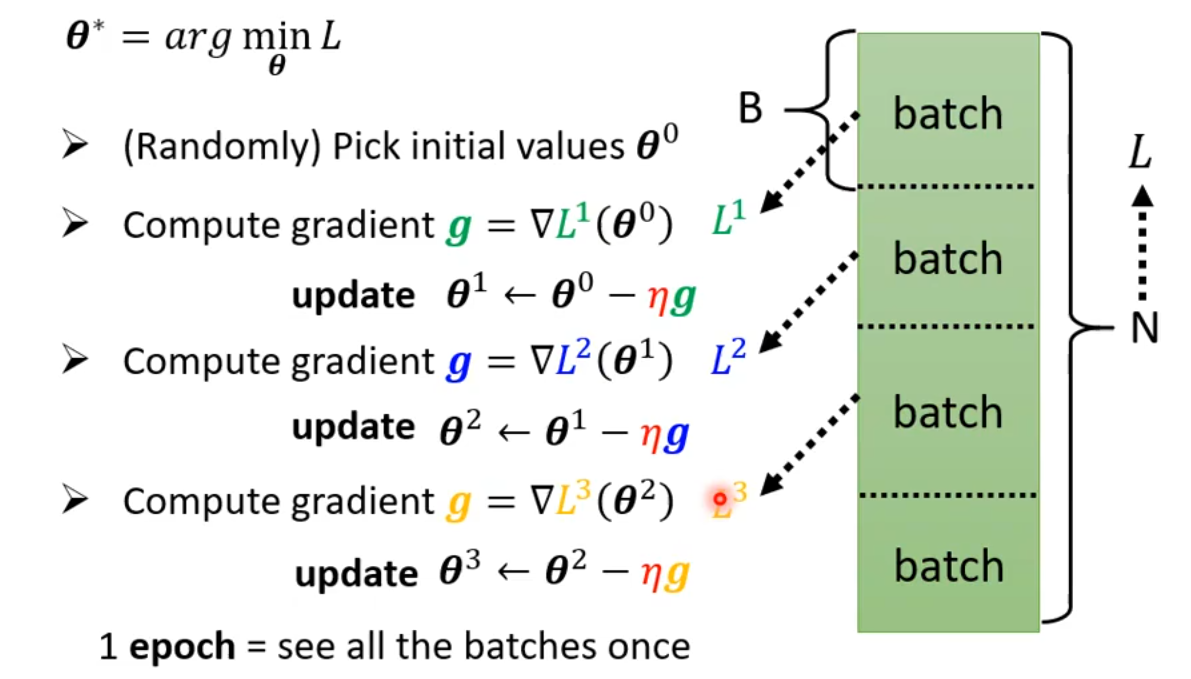
batch:N条数据随机均等切分,每一份是一个batch;
batch size:每份batch的大小,这是一个超参数;
update:每计算一次梯度更新一次参数,成为一次update;
epoch:模型每次完整地看到所有的batch,称为1 epoch。(这里的“看到”,也可以换成“扫过”、“遍历”等词语表达)
举例:

一旦找到了最佳的\boldsymbol \theta^* = arg \min_{\theta}L,也就训练好了模型。
6 激活函数(Activation Function)
我们回顾一下sigmoid函数,它是一个“S”型函数。我们在上文中一直在使用sigmoid函数,那可不可以使用 Hard Sigmoid 呢?其实是可以的。
如何表示 Hard Sigmoid 的曲线呢?我们可以使用两个 Rectified Linear Unit(ReLU)的函数之和来表示 Hard Sigmoid。ReLU是一个两段曲线,前一部分与x轴重合,,后一部分是射线。其表达式为:c \space max(0, b+wx_1)。
如下图所示,两个Relu相加可以组成一个 Hard Sigmoid 。
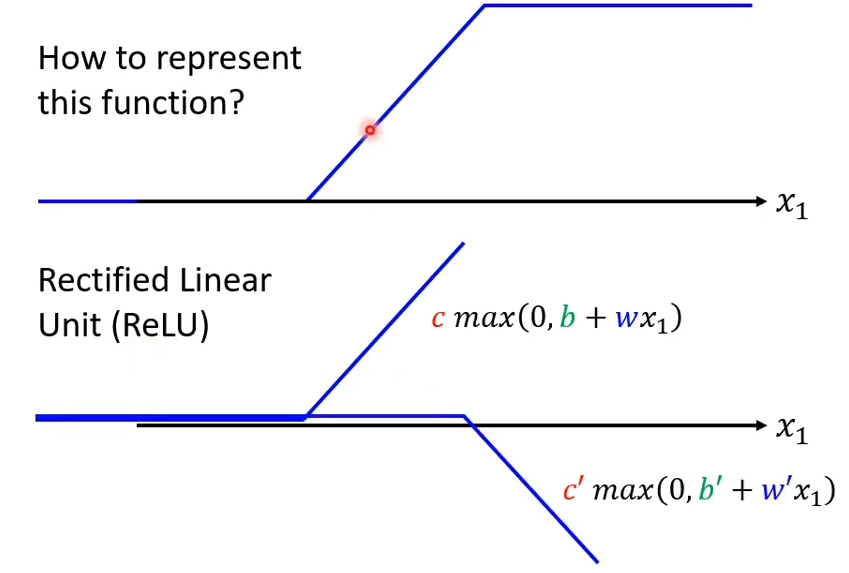
于是,我们可以使用ReLU来替换模型中的sigmoid:
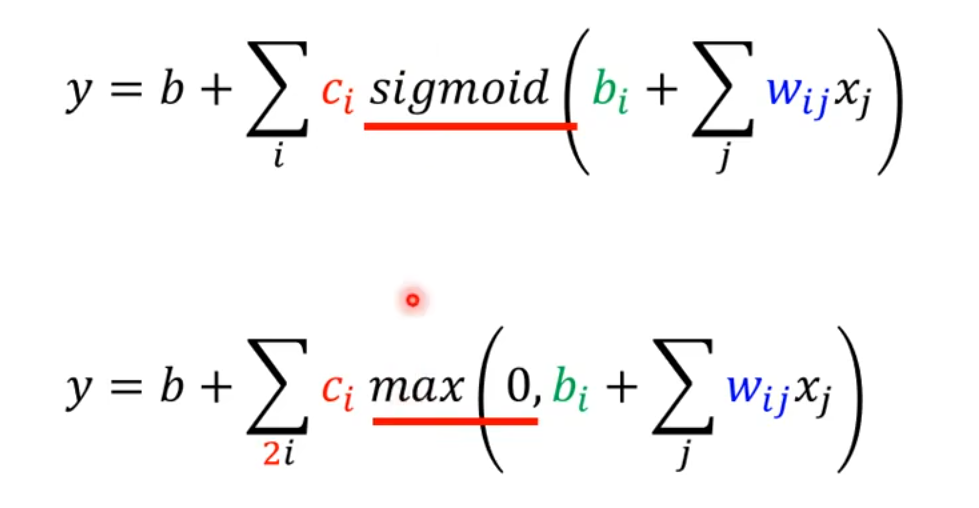
在机器学习中,sigmoid和ReLU这样的函数,称之为激活函数(Activation Function)。在大多数深度学习任务中,ReLU通常表现得更好。接下来的例子都将使用ReLU。
在真实的数据上,我们得到以下结果:

可以看出使用ReLU明显比linear效果更好。1000ReLU相比100ReLU虽然在训练数据上有轻微差异,但在测试数据上没有进一步的提升,所以不需要进一步增加ReLU了。
7 进一步改进模型
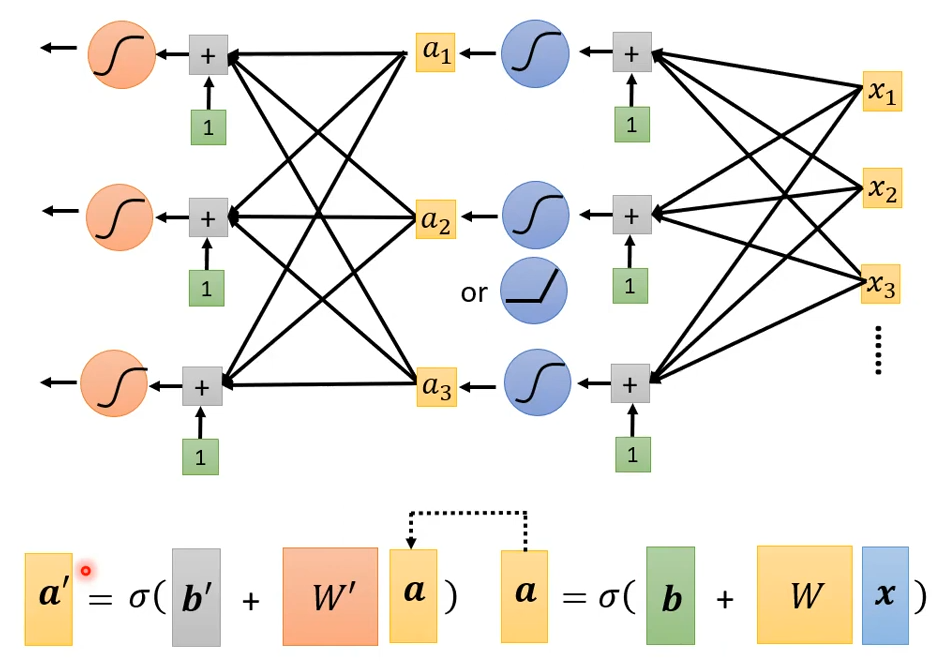
到目前为止,我们的模型看起来已经非常专业了,并且模型的预测效果也在不断地提升。让我们回顾一下上文的向量\boldsymbol a:
当然这里的\sigma ()也可以换成ReLU()。我们对于feature \boldsymbol x计算出了\boldsymbol a,此时我们可以将这个\boldsymbol a看作是新的feature,再套一层\sigma (),甚至可以套多层。具体套几层,这也是一个超参数。
我们来看看使用不同层的模型结果:
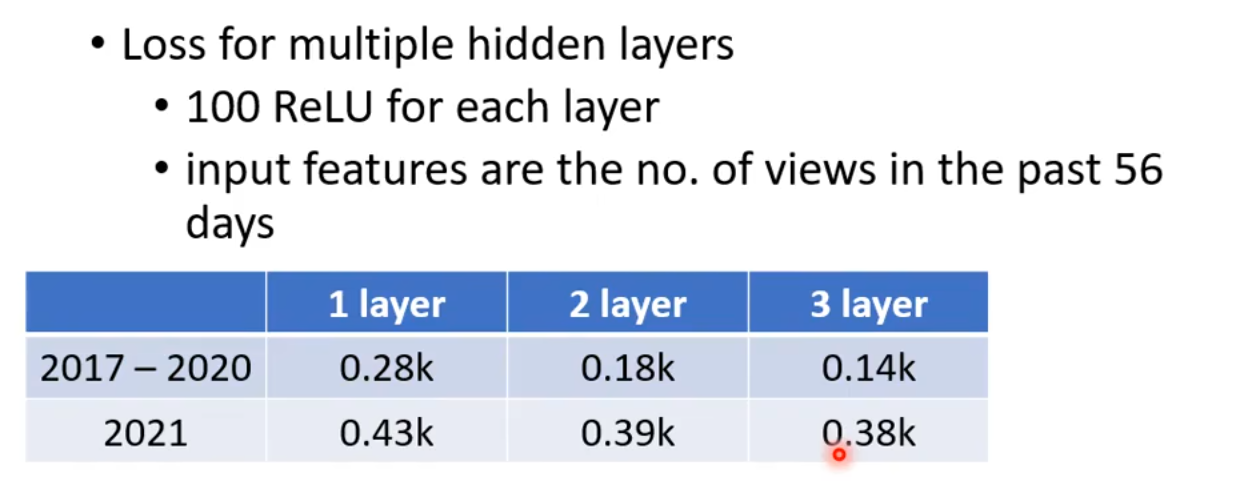
很显然,多层收获了更好的效果。
8 神经元和隐藏层
巫师需要对自己的工具取高大上的名称,才能够唬住麻瓜。
神经元(Neuron):即上文中的\boldsymbol a;
神经网络(Neurual Network):有神经元的网络,称之为神经网络。(“网络”、“模型”、“网络模型”基本是混着用,是一个意思)
隐藏层(Hidden Layer):同一层的神经元,构成一个隐藏层;
深度学习(Deep Learning):有多个隐藏层的网络,称之为深度学习网络。
我们来看看近些年来的深度学习网络,图中的红色百分数指的是错误率:
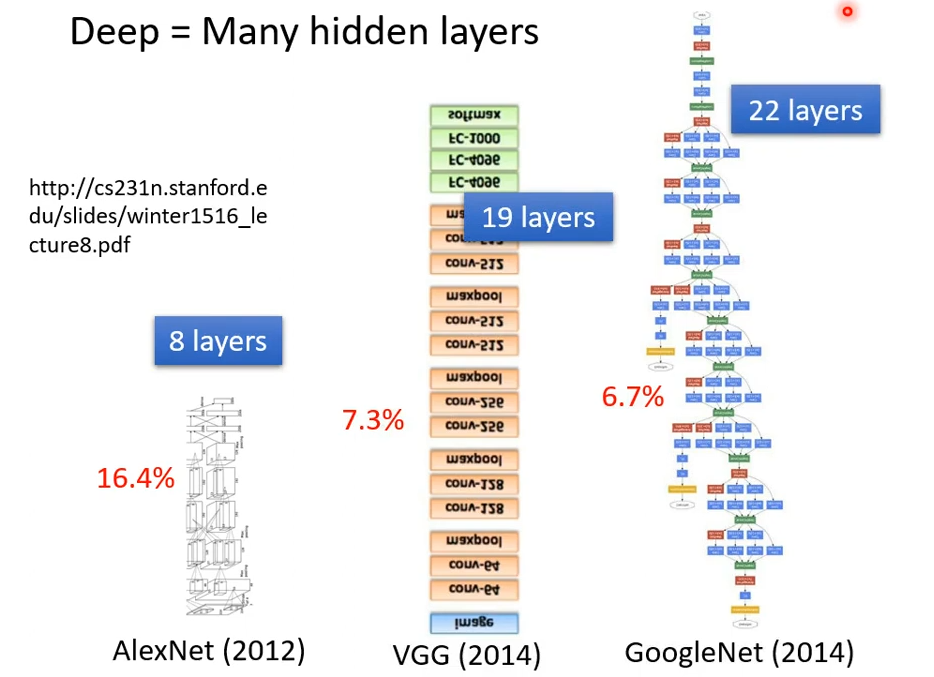
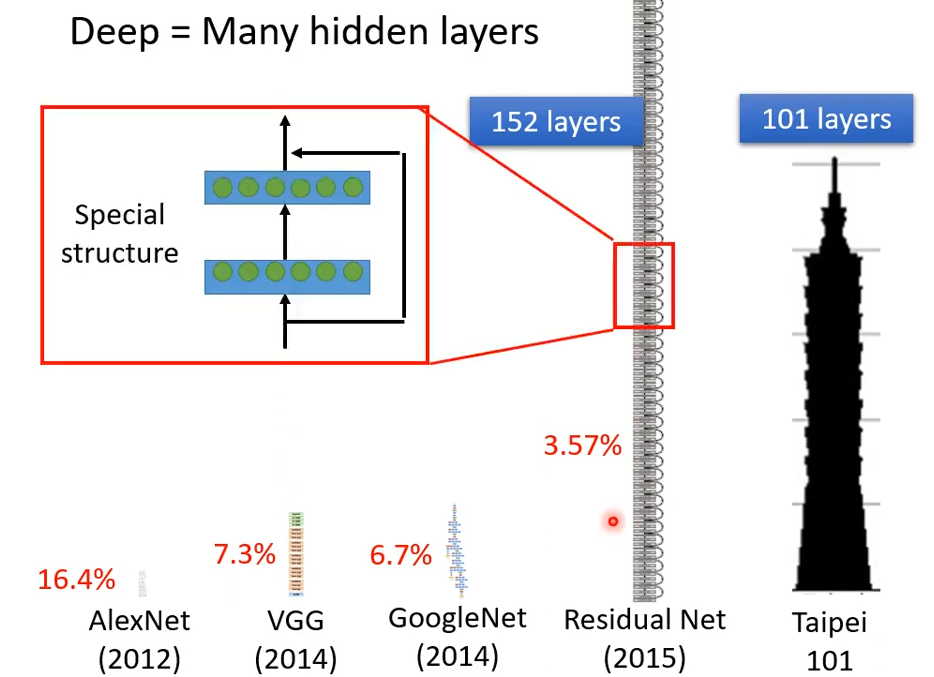
到了残差网络(Residual Net)这里,已经到了152层了。现在没个几百层都不好意思说自己是deep learning。那么层数是越多越好吗?
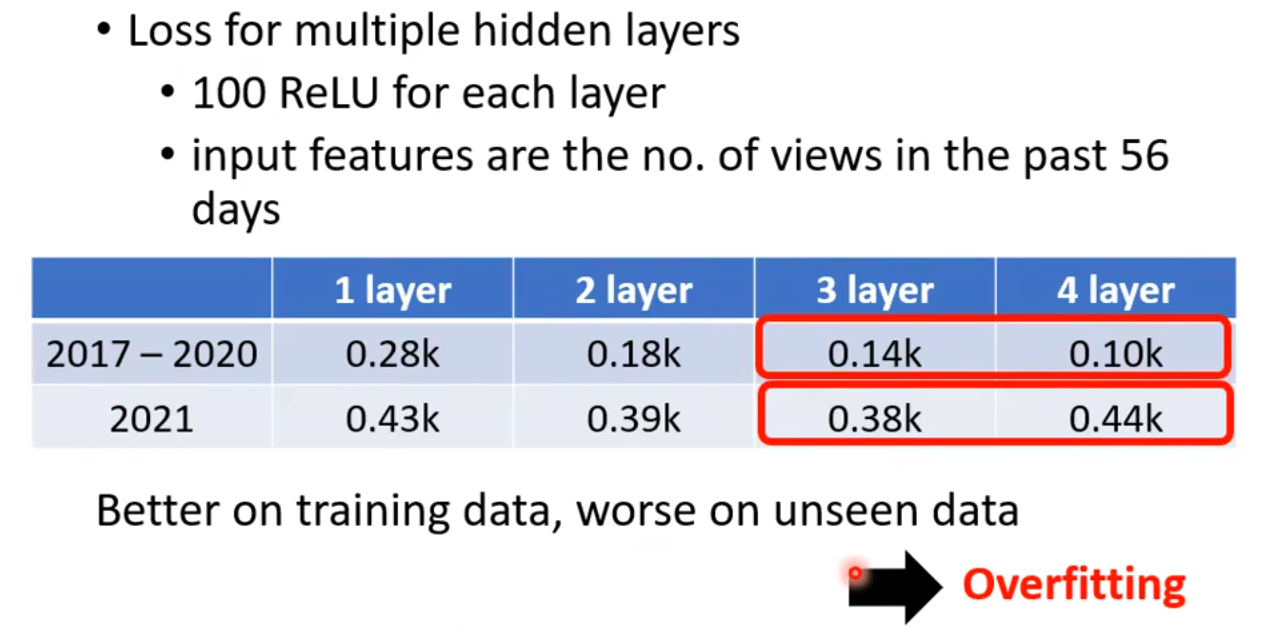
9 过拟合(Overfitting)
我们来继续加深层数,4层的模型相比于3层的模型,虽然对于训练数据上loss更小,但是在测试数据上的loss更大。这意味着4层网络的预测效果反而更差。这种现象成为过拟合(Overfitting)。很显然,我们应该选择3层的模型,并不是越deep越好。
10 思考
我们在学习sigmoid或者ReLU的时候,提到过使用多少sigmoid或者ReLU是一个超参数。使用越多理论上就能更好地拟合真实的数据。为什么我们后来还要套很多层呢,为什么不将一层做得很精细呢?一层套一层似乎没道理呀,为啥\boldsymbol a就能再次作为feature呢?
难道就因为deep net听起来更高级,而只做一层就很fat,fat net就很低级?继续深入学习吧,如果不deep学习,那说明你就在fat学习。而事实上,deep学习要比fat学习更好。


评论区