1 Review: Optimization with Batch

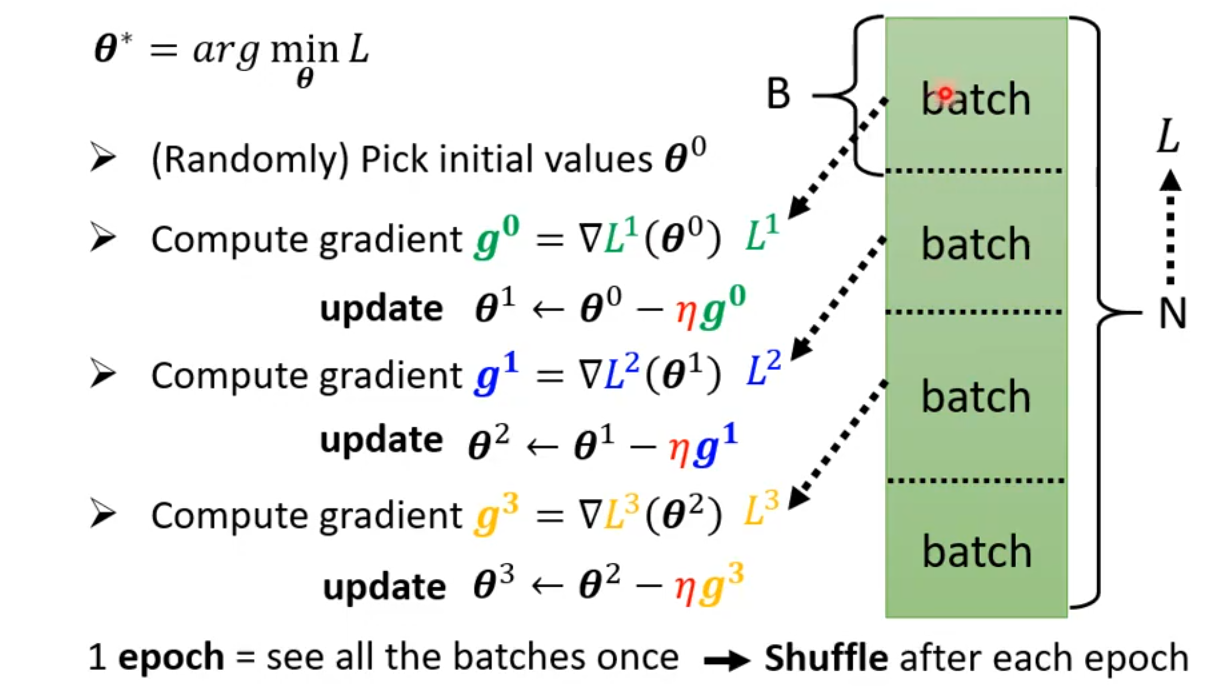
每一个epoch之后，都要shuffle数据，重新分batch，再进行下一个batch。

2 Small Batch v.s. Large Batch

理论分析（不考虑GPU的并行计算）：

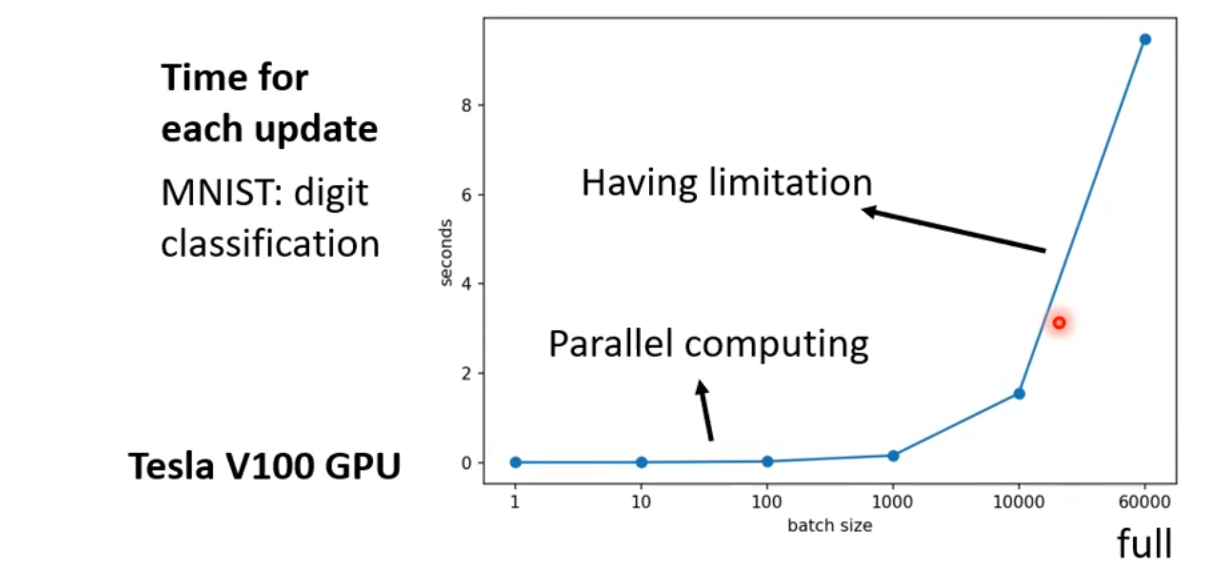
实际上，large batch size 不一定需要更长的时间去计算梯度，因为GPU可以并行计算。但是如果batch size非常大，超出了GPU的并行计算能力，也是会需要很长的时间。

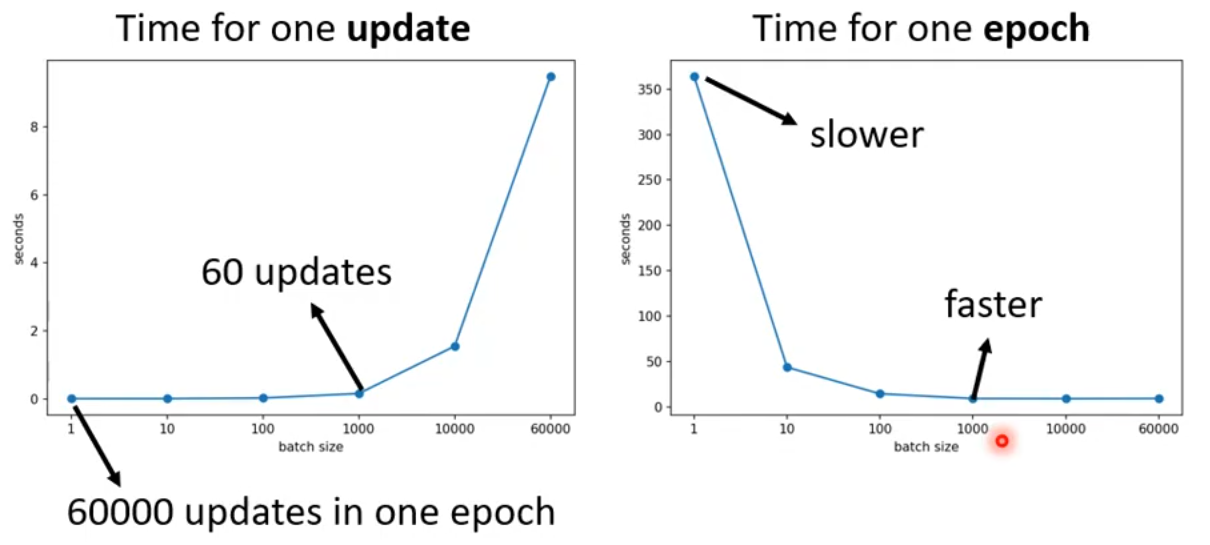
考虑GPU的并行计算，对于一次完整的epoch，small batch size 需要更长的时间，反而large batch size需要更少的时间。

到目前为止，我们的分析倾向于 large batch size，因为它的训练时间更少。但是，在实际的训练任务中，small batch size 有更好的训练效果。

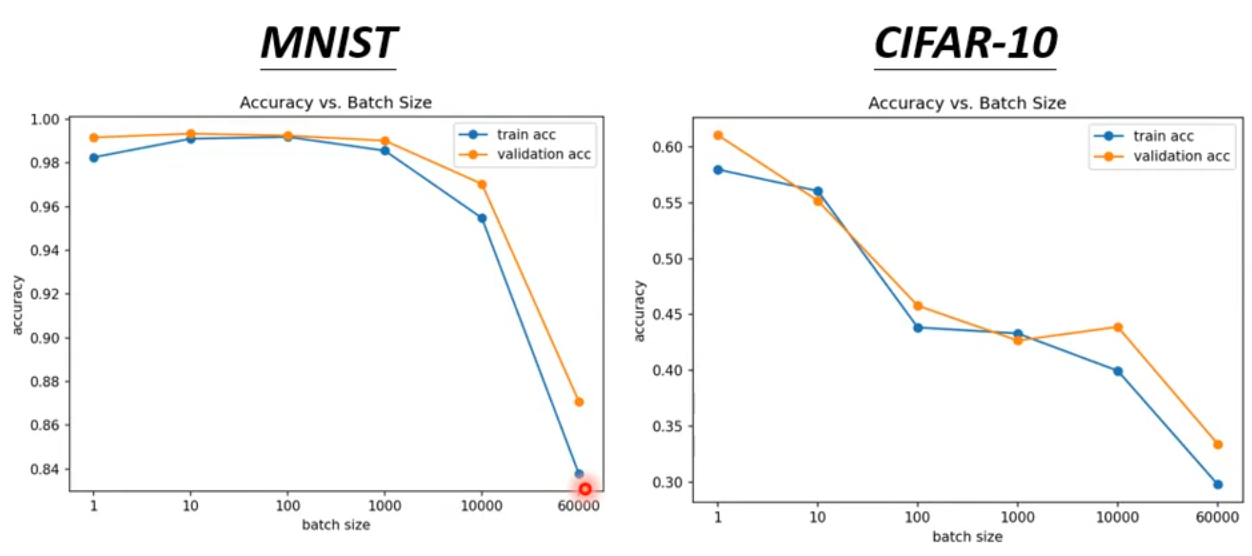
但是 large batch size 哪里出现了问题了呢？是因为 large batch size 更容易被 Optimization Issue 阻塞住，而 small batch size 通常能更顺利地进行 Optimization。

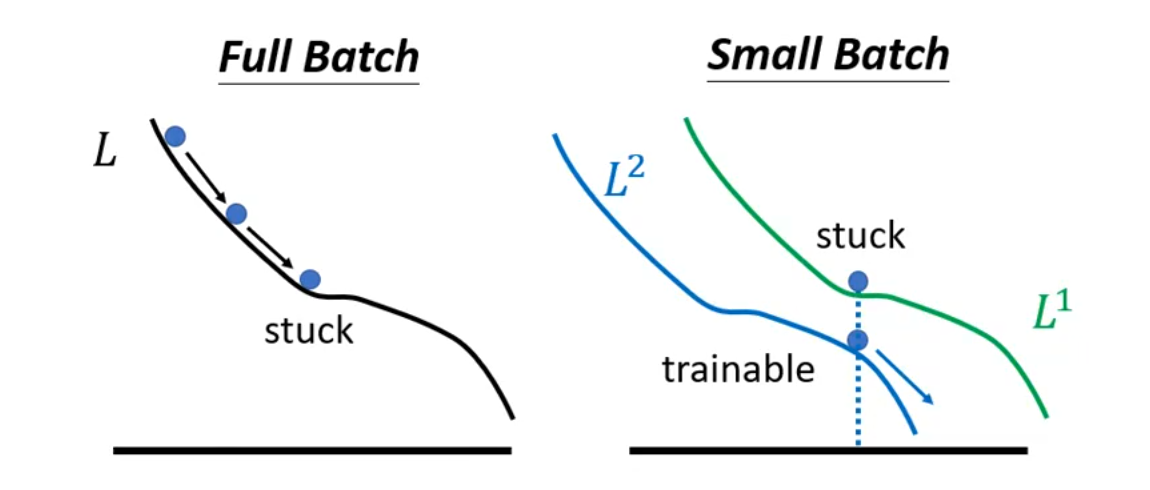
此外，即使 small batch size 和 large batch size 在训练数据上的效果相同，但是 small batch size 在测试数据上仍有优势。

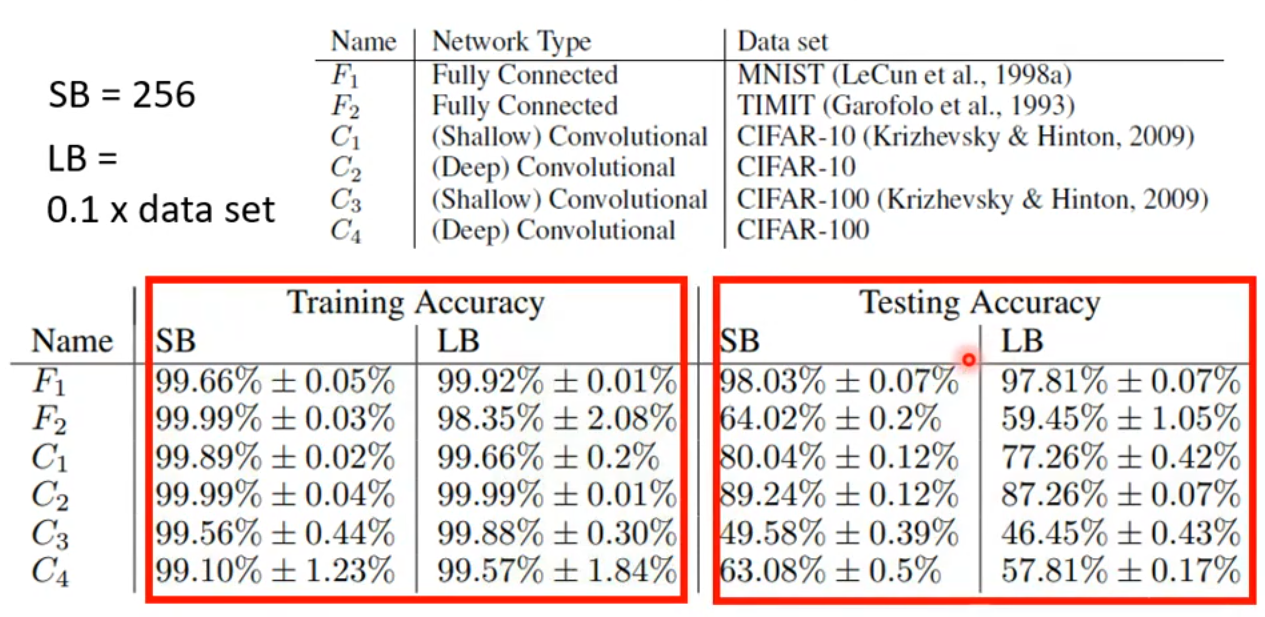
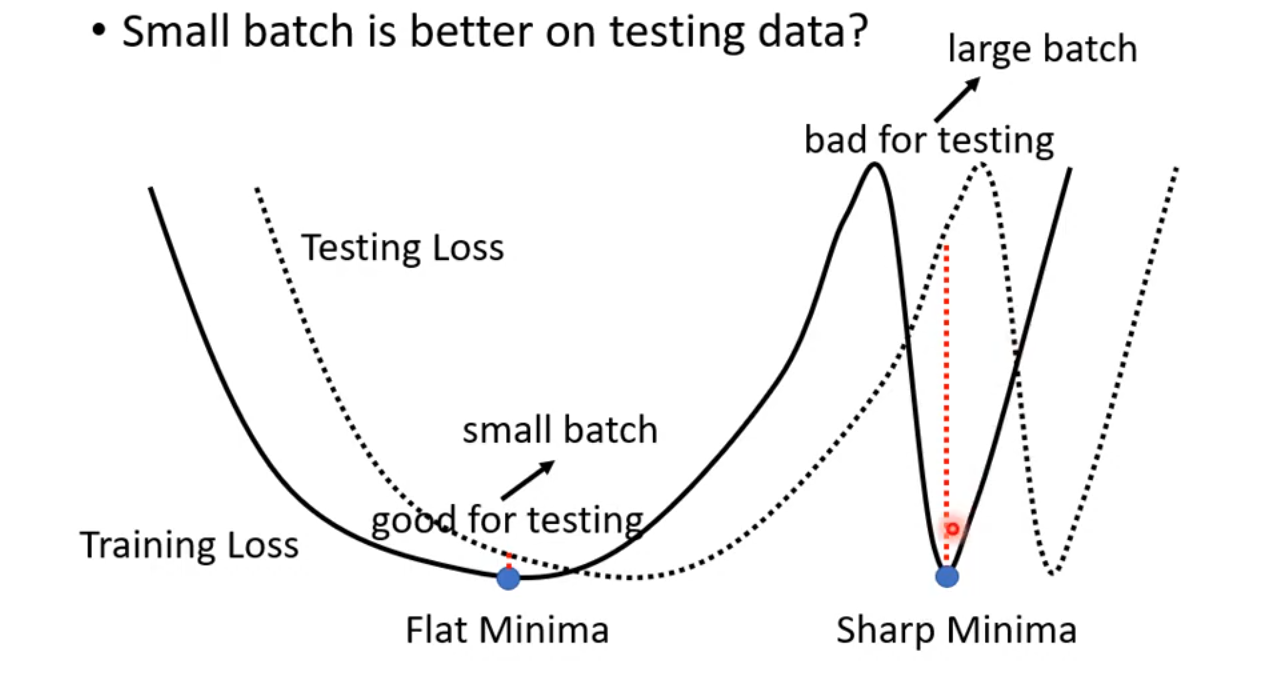
有一种解释是，训练中，small batch size 倾向于 Flat Minima，而 large batch size 倾向于 Sharp Minima，而由于测试数据和训练数据的分布存在差异，一点点的分布差异，对于 Flat Minima 来说，结果差异很小，但是对于 Sharp Minima 来说，结果差异就会很大，从而造成更大的loss。

small batch size 和 large batch size的对比：

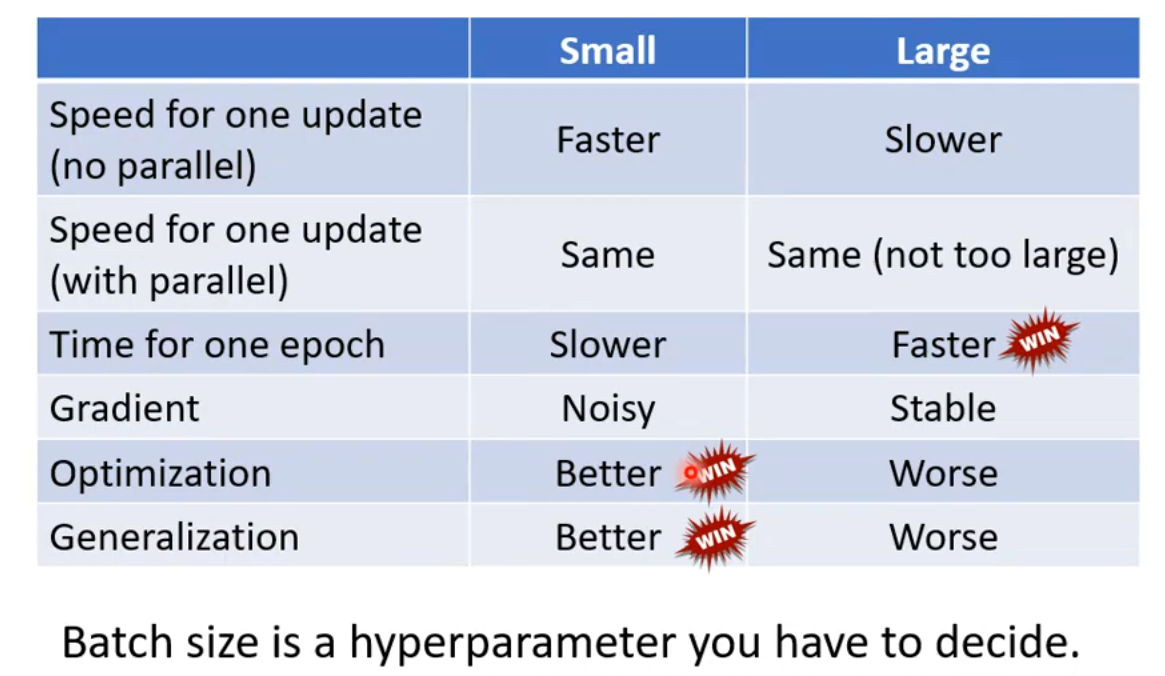
作为模型训练者，既想要 large batch size 的训练速度，又想要 small batch size 的效果，怎么办呢？有许多研究者讨论这个问题，也有许多解决方案，这里仅作了解即可。

3 Momentum

我们可以将loss函数的曲线看作是小球滚动轨迹，即使遇到平滑的地方，小球由于惯性依然往前运动，即使遇到了上坡，由于惯性，小球仍可以继续运动。Momentum 翻译为动量，刚刚说的”惯性“，也可以换成“动量守恒”。但这些都只是描述梯度下降的性质而已，并没有真实模拟物理规律，只是给这种梯度下降起了一个看起来贴切又高级的名字。那这种梯度下降具体是什么呢？

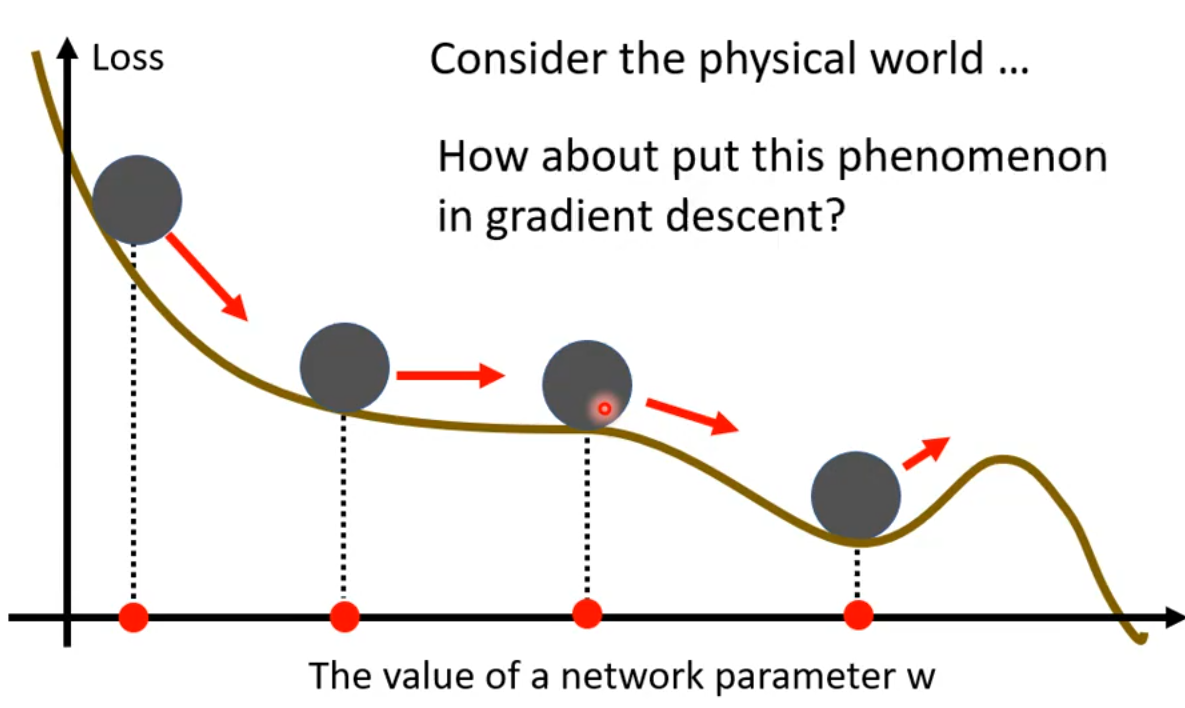
3.1 普通的梯度下降

每次计算梯度后，向梯度的反方向更新参数。

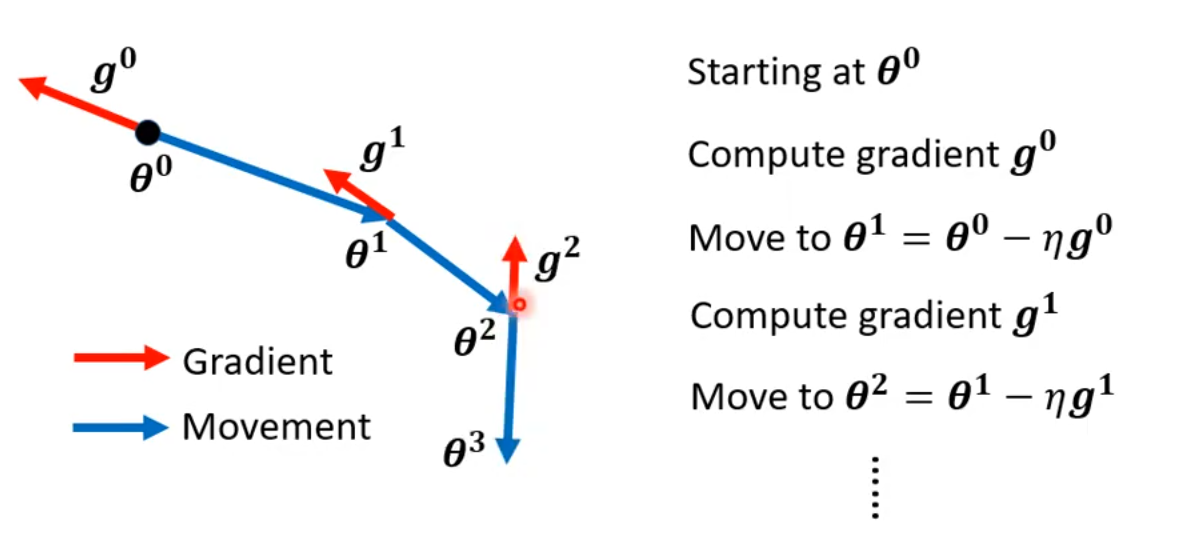
3.2 普通的梯度下降 + momentum

每次计算梯度后，结合本次的梯度和上一次的梯度，再更新参数。移动方向是上次的方向减去本次的梯度。

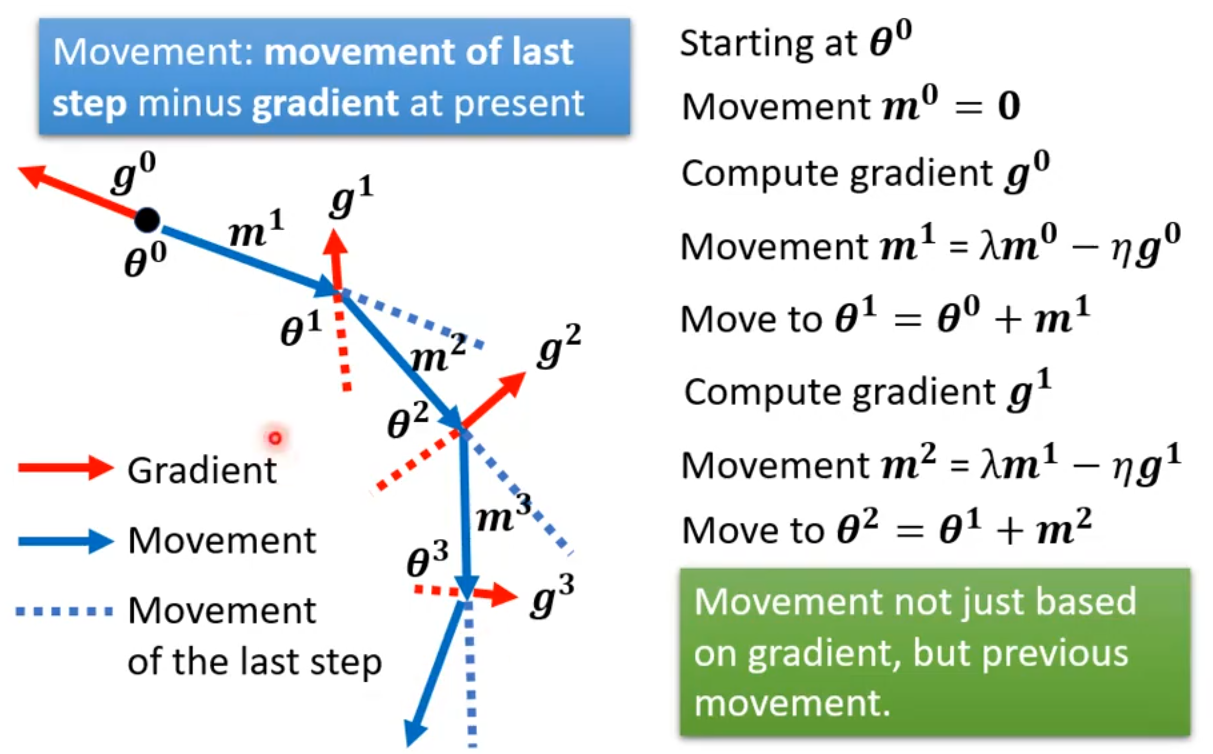
由于每次的更新方向都与上一次的方向有关，就相当于每一次的更新方向与之前每一次的方向都有关。更新方向由梯度决定，所以每次的更新方向可以用所有之前的梯度来表示：

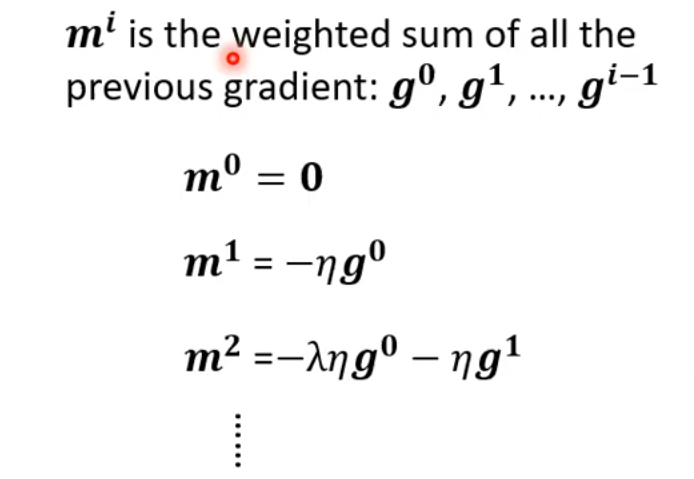
我们来看一个例子：

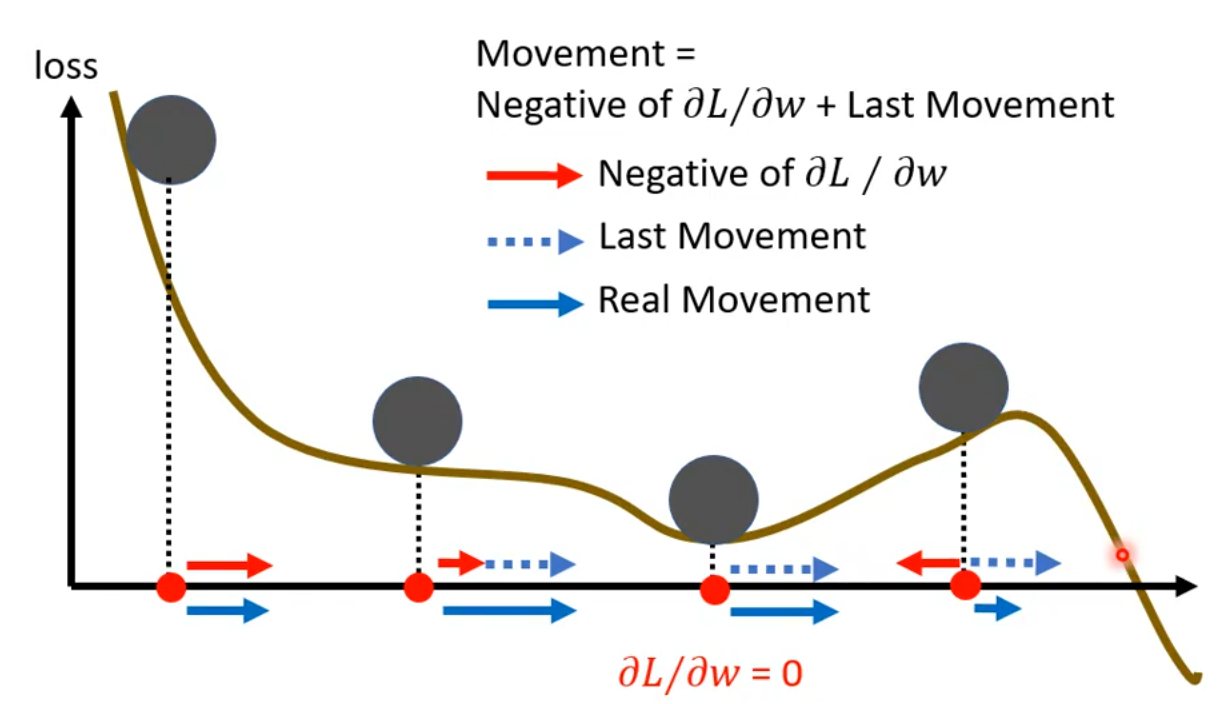
由于引入了 Momentum，在梯度下降的时候：

即使遇到平滑的地方，也会受上一次梯度的影响而快速渡过；

即使遇到了 local minima，也会因为引入上次的梯度而能够继续更新；

即使遇到了上坡，也会因为引入上次的梯度而可能越过这个坡。

4 Conclusion

在 critical point 的梯度为0；

critical point 可以是 local minima 或 saddle point；

在实际训练中 local minima 是很罕见的；

small batch size 和 momentum 能够帮助模型在进行梯度下将时逃出 critical point。