1 什么是机器学习？

Machine Learing 约等于 Looking for Function。

示例：

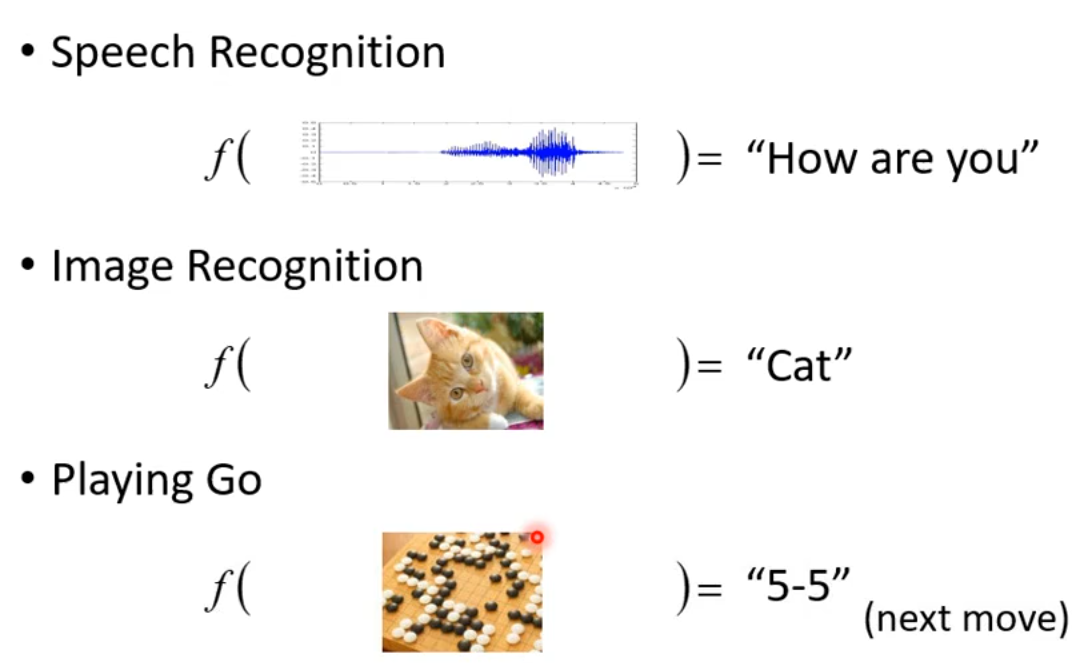
2 不同类型的Functions

2.1 回归（Regression）

函数输出一个数值。

示例：

预测第二天的PM2.5数值：

2.2 分类（Classification）

给定选项（或者称为类别），函数输出数据对应的正确的类别。

示例：

垃圾邮件分类：

象棋落子位置：

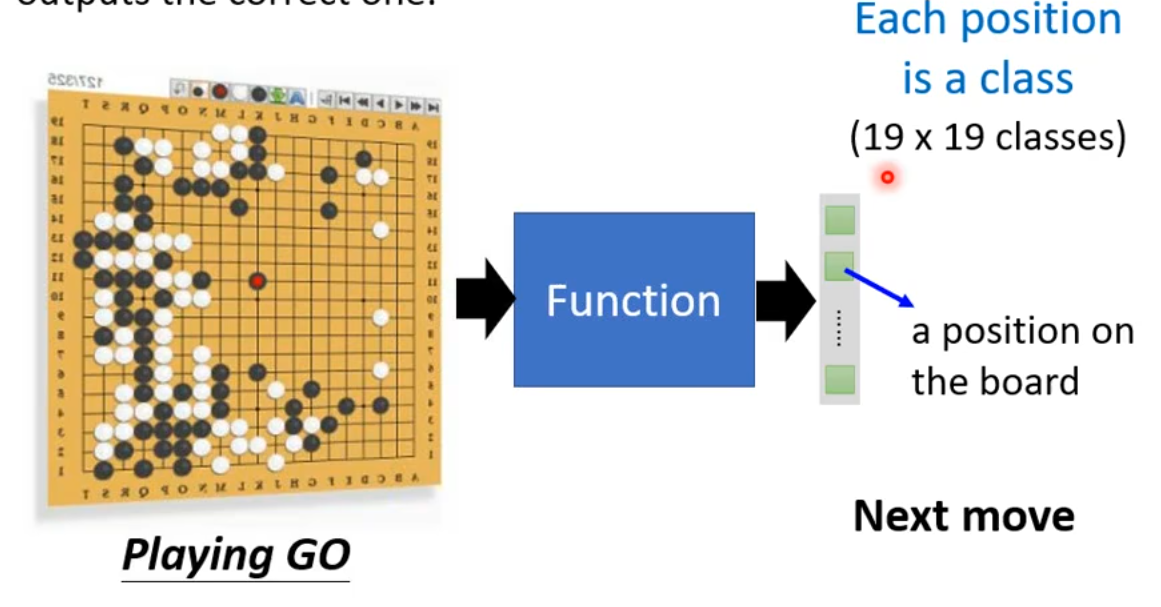
2.3 Structure Learing

创造数据。比如生成图片、文档等。先了解即可。

3 How to find a function?

以一个例子来讲解：

给定某个youtube频道历史每天的观看数据量，预测下一天的观看数据。

3.1 写出带有未知参数的function

如何写出这个function呢？对于一个小白来说，大脑是一片空白；但是对于一个专业人士，脑子里会有相关领域的知识，对于自己领域内的问题可以猜测。

这个例子比较简单，我作为一名专业的网上冲浪选手，凭借着与生俱来的网感，我猜测youtube频道的观看数据跟前一天的观看数据可能有千丝万缕的关系，所以我猜测这个function为：

y=b+wx_1

其中，x₁为前一天的数据，y为后一天的数据，w和b是未知参数，需要从已有的数据中学习得到。

model：我们常听到的模型就是这里的y=b+wx_1
feature：特征指的是这里的已知数据x1
weight：权重值的是这里的w
bias：偏差指的是这里的b

3.2 定义损失函数（loss function）

损失是对于未知参数的函数：L(b, w)。
损失是用来评估某组未知参数的好坏。

假设我们将未知参数设置为 b=0.5k（这里的k是一千的意思），w=1（通常在训练开始时，这里是随机值）。即：

y=0.5k+1x_1

接下来我们就开始评估这组参数的好坏。

这是训练数据：

以2017.01.01的观看数据4.8k为例，预测下一天的观看数据为：

y=0.5k+1x_1=0.5k+1*4.8k=5.3k

但是下一天的真实数据为 \^{y}=4.9k，所以可以计算出预测值和真实值的差值：

e_1=|y-\^{y}|=0.4k

label：真实值，即这里的\^{y}。

同理可以计算出差值e_2,...,e_N：

最终我们可以计算对于参数b=0.5k、w=1这组参数的Loss：

Loss: L=\frac{1}{N}\sum{e_n}

目前了解即可：
if e=|y-\^{y}|，L is mean absolute error(MAE);
if e=(y-\^{y})^2，L is mean square error(MSE);
if y and \^{y}are both probability distributions ==> Cross-entropy

Loss的温度图：

颜色越红代表loss越大。

3.3 优化（Optimization）

最优的参数为：

w^*,b^*=arg\min_{w,b}L

假设我们只有一个未知参数w，找出最佳的w^*，即w^*=arg\min_{w}L。
我们正式引入梯度下降（Gradient Descent）：

随机选取初始值w^0;
计算微分\frac{\partial L}{\partial w}|_{w=w^0}；如果结果为负（Negative），则增加（Increase）w；如果结果为正（Positive），则减小（Decrease）w；
接下来就需要更新w了，从w^0更新到w^1。更新的步长为\eta\frac{\partial L}{\partial w}|_{w=w^0}，即：
w^1 \leftarrow w^0 - \eta\frac{\partial L}{\partial w}|_{w=w^0}

其中\eta是学习率（learning rate），这是一个超参数（hyperparameters）。

什么是超参数？简单来说，就是认为给定的一个固定值的参数，我们经常说“调参侠”，可以简单理解为改一改超参数的值，看看模型效果有没有变好。

我们来看这张图，图中是L对w的函数。（这个曲线是随便画的，按照我们上面的Loss计算公式，应该满足 L \ge 0但是Loss函数多种多样，可以自己选定，有的Loss允许 L < 0。)

更新w到什么时候停止呢？

可以人为指定更新次数，比如一百万次；
当计算的微分为0时；

这里可以很明显得发现，如果初始随机的w在图中的w^0，则到w^T时就停止更新参数了。但是此时找到的L是局部最小值，而不是全局最小值。

剃度下降存在局部最小值问题。不过这应该可以通过某些算法优化或者避免，剃度下降的核心问题另有其”问题i“，这里只做了解即可。

上述内容是假设只有一个未知参数w，对于多个未知参数，步骤是一样的：

随机选取初始值w^0, b^0;
计算微分\frac{\partial L}{\partial w}|_{w=w^0, b=b^0}, \frac{\partial L}{\partial b}|_{w=w^0, b=b^0};
更新参数：
w^1 \leftarrow w^0 - \eta\frac{\partial L}{\partial w}|_{w=w^0, b=b^0} \\ \space \\ b^1 \leftarrow b^0 - \eta\frac{\partial L}{\partial b}|_{w=w^0, b=b^0}

3.4 阶段性小结

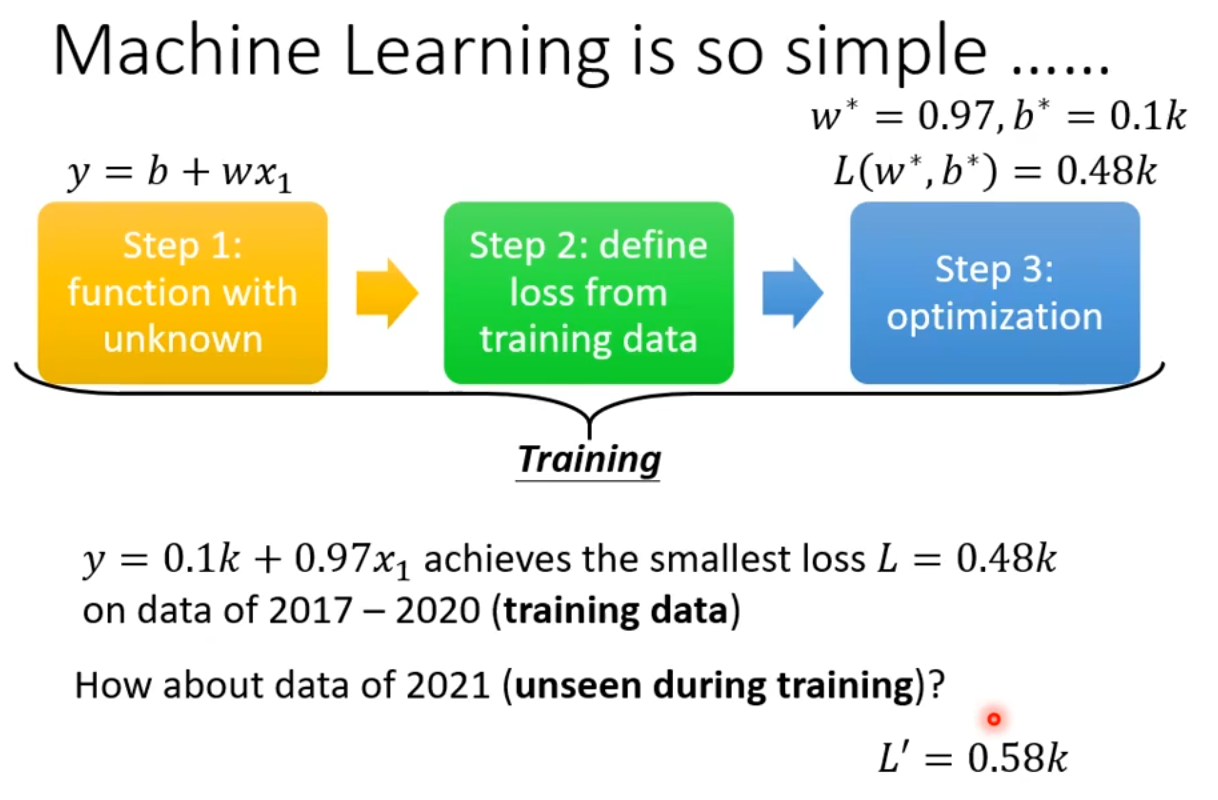
训练数据为2017-2020的数据，最终最佳的w=0.97k、b=0.1k，该组参数对应的L=0.48k。

用训练得到的模型，在2021年的数据上做验证，得到L=0.58k。只看这个0.58k其实除了稍微上升也看不出什么门道，画图看一看：

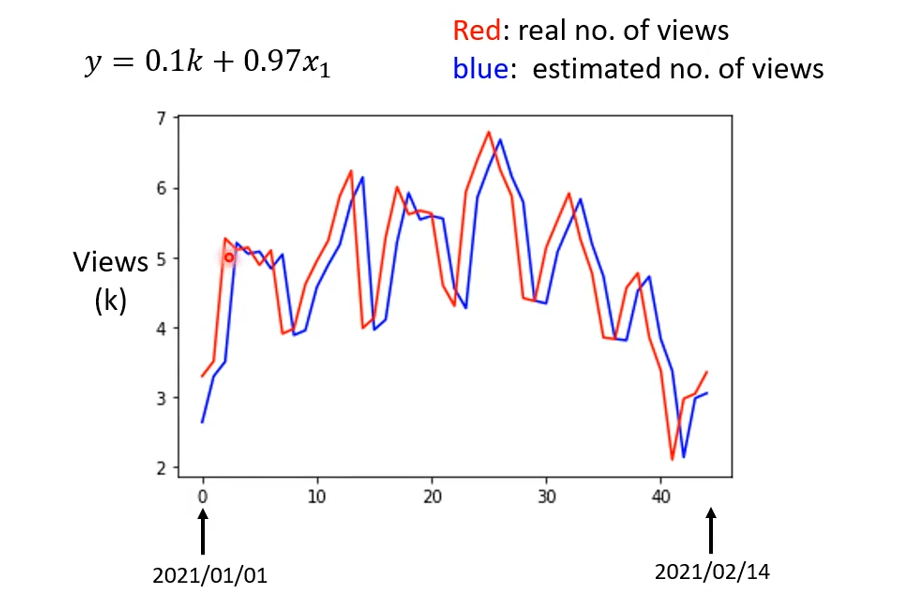
观察图中红蓝线，基本是红线向右移动一点就是蓝线。这说明模型基本是用前一天的数据作为预测后一天的数据。对于平缓的数据，这样没什么问题，对于跳动有峰值的数据，就会出现将前一天的峰值，作为后一天的预测值，而后一天很可能比峰值小的多。

观察图中的数据分布（只看红线），大约每7天中，有两天的数据会突然下降。所以我们可以认为每隔7天是一个周期，从而去继续优化模型。（这个步骤就体现出了领域专家的作用，专家可能能够发现潜在的因素帮助优化模型）

3.5 进一步优化模型

原先的模型只考虑前一天的数据对后一天的数据的影响，但是经过上述观察，我们猜测7天为一个周期，于是考虑前7天的数据对后一天的数据的影响。

将原来的模型：

y=b+wx_1

更新为：

y = b + \sum_{j=1}^7 {w_jx_j}

新模型的最佳参数和loss为：

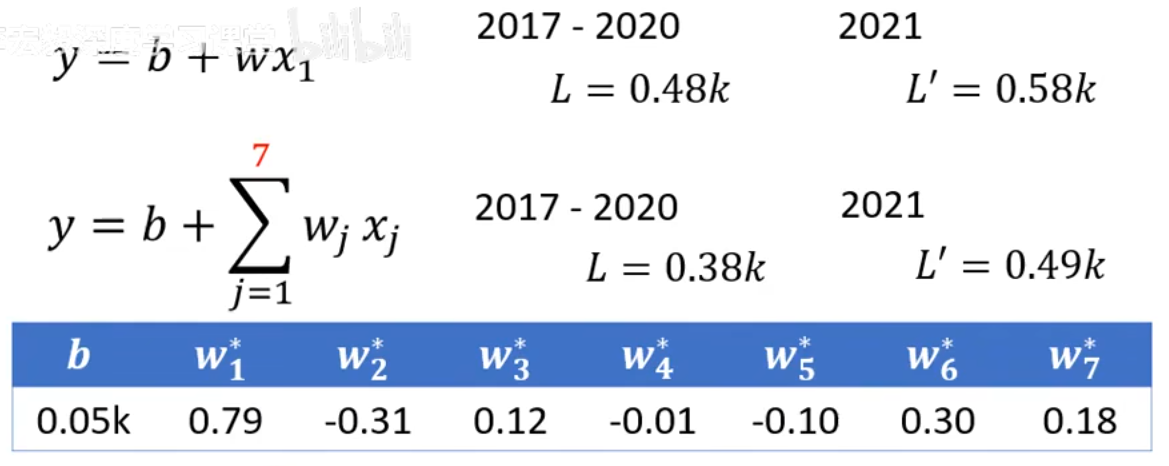
可以看出，在训练数据上（2017-2020），loss从0.48k降低到了0.38k，在测试数据上（2021），loss从0.58k降低到了0.49k。这意味着新的模型有更高精度的预测能力，模型的效果有了明显提升。

进一步地，既然考虑前7天的数据效果更好，我们可以将该方法泛化，考虑前多天的数据：

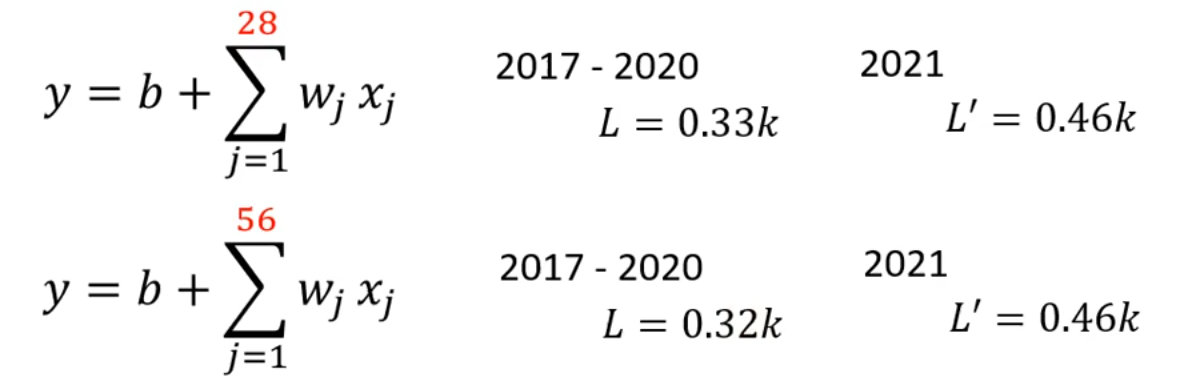
考虑前28天数据的影响，loss的效果更好了；考虑前56天数据的影响，在训练数据上loss有轻微优化，在测试数据上loss不变。这说明我们很可能已经逼近最优模型了。

上述这些对于feature（x）乘以权重（w），再加上偏差（b）的模型，成为线性模型（Linear models）。这种模型还是比较简单的，随着接下来学习的深入，我们将会接触到更多更复杂的模型。

目录CONTENT

第一节（上）：机器学习基本概念